1.1 DRL基础
概率论复习
随机变量
- 随机变量是概率论和统计学中的一个重要概念,它用来描述随机试验的结果。
- 随机变量可以分为两大类:离散型随机变量和连续型随机变量。
- 离散型随机变量: 这种随机变量的取值是可数的,通常是整数。例如,抛一枚骰子,随机变量可以是骰子的点数,取值范围为1到6。离散型随机变量的概率分布可以通过概率质量函数(Probability Mass Function,PMF)来描述,它给出了随机变量每个可能取值的概率。
- 连续型随机变量: 这种随机变量的取值是不可数的,通常是实数。例如,测量一件物品的长度,随机变量可以是任意实数值。连续型随机变量的概率分布可以通过概率密度函数(Probability Density Function,PDF)来描述,它表示在某一点附近的概率密度,而实际概率则是通过对概率密度函数进行积分得到。
- 无论是离散型还是连续型随机变量,它们都可以用来描述随机现象的不确定性,以及在概率论和统计学中进行推断和分析。
- 在使用随机变量时,我们通常关注以下几个方面:
- 分布函数(Cumulative Distribution Function,CDF): 描述随机变量小于或等于某个特定值的概率。
- 期望值(Expectation): 表示随机变量的平均值,反映了分布的中心位置。
- 方差(Variance): 衡量随机变量取值的分散程度,即分布的宽窄程度。
- 随机变量和概率密度函数或概率质量函数的概念在概率论、统计学、以及应用领域如机器学习等方面都扮演着关键的角色。
概率密度函数
概率密度函数(Probability Density Function,简称PDF)是描述随机变量在各个取值上的概率分布的数学函数。对于连续型随机变量,概率密度函数是定义在整个实数轴上的非负函数,其满足以下两个条件:
- 对于任意实数x,概率密度函数f(x)都是非负的:\(f(x) \geq 0\)
- 整个实数轴上的概率密度函数的积分等于1:\(\int_{-\infty}^{\infty} f(x) \, dx = 1\)
这两个条件确保了概率密度函数对于所有可能的取值都提供了非负的概率,并且整个概率空间的总和是1。
对于一个连续型随机变量X,它落在某个区间a , b上的概率可以通过对概率密度函数在该区间上的积分来计算:\(P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx\)
需要注意的是,概率密度函数并不直接给出具体的概率值,而是在某个取值范围内的概率密度。概率密度函数的图形在某个区间上的曲线下方的面积表示该区间内的概率。
常见的概率密度函数包括正态分布、指数分布、均匀分布等。每种分布有其特定的数学形式和性质,适用于不同类型的随机现象建模。
数学期望
数学期望(或均值)是随机变量的一个重要性质,它用来描述随机变量的平均值。对于一个离散型随机变量X,其数学期望(期望值)表示为E(X),定义如下:
\(E(X) = \sum_i x_i \cdot P(X = x_i)\)
对于一个连续型随机变量X,其数学期望表示为E(X),定义如下:
\(E(X) = \int_{-\infty}^{\infty} x \cdot f(x) \, dx\)
其中,\(x_i\)是离散型随机变量X的可能取值,\(P(X = x_i)\)是相应取值的概率。对于连续型随机变量X,f(x) 是其概率密度函数。
数学期望的直观理解是随机变量在长期重复试验中的平均值。它是一个对分布中心位置的度量,反映了随机变量的集中趋势。
数学期望具有一些性质,例如:
- 线性性质: 对于常数a和b以及随机变量X、Y,有\(E(aX + bY) = aE(X) + bE(Y)\)
- 独立性质: 如果X和Y是相互独立的随机变量,则\(E(XY) = E(X)E(Y)\)
数学期望在概率论和统计学中有广泛的应用,它不仅用于描述随机变量的平均值,还在推断、决策理论等领域中发挥着重要作用。
随机抽样
随机抽样是一种用来选择样本的方法,其中每个个体有相等的机会被选中,从而确保样本是代表总体的。随机抽样是统计学中的基本概念,它有助于减小选择偏差,使样本更具有代表性,从而更好地反映总体的特征。
以下是一些常见的随机抽样方法:
- 简单随机抽样: 在简单随机抽样中,每个个体被选中的概率是相等的,且每个样本的选择是独立的。这通常通过随机数生成器来实现,确保每个个体都有等概率地进入样本。
- 分层随机抽样: 将总体划分为若干层(或称为分层),然后在每个层内进行简单随机抽样。这样可以确保每个子群体在样本中都有代表性,特别适用于总体内存在明显差异的情况。
- 系统随机抽样: 选择一个随机的起始点,然后按照一个固定的步长或间隔进行抽样。这种方法适用于总体中个体的排列是有规律的情况。
- 整群抽样: 将总体划分为若干群,然后随机选择一些群,再从选中的群中抽取所有个体。这种方法适用于总体内群与群之间存在相似性,但群内个体差异较大的情况。
- 多阶段抽样: 将抽样过程分为多个阶段,每个阶段在前一阶段的基础上进行抽样。这种方法适用于总体内存在层级结构的情况。
随机抽样的目的是确保样本是随机的、无偏的,从而使样本结果对总体具有代表性。这有助于推断性统计分析,使得通过样本的结果能够对总体的特征进行推断。
强化学习专业术语
state 和 action
在强化学习中,状态(state)和动作(action)是两个关键的概念,它们用于描述智能体(agent)与环境(environment)之间的交互和学习过程。
- 状态(State): 状态是描述系统或环境的特定瞬时条件的表示。在强化学习中,状态是智能体观察到的关键信息,它包含了有关环境的所有必要信息,以便智能体可以做出决策。状态可以是离散的或连续的,具体取决于问题的性质。智能体的策略和动作通常依赖于当前的状态。
- 动作(Action): 动作是智能体基于当前状态所采取的行为或决策。在强化学习中,智能体从可选的动作中选择一个来影响环境,并进入新的状态。动作可以是离散的,例如在棋盘游戏中的移动一枚棋子,也可以是连续的,例如在机器人控制中的连续运动。
在强化学习的框架中,智能体与环境之间的互动通常可以描述为一个序列的状态、动作、奖励(reward)和下一个状态。这被称为马尔可夫决策过程(Markov Decision Process,MDP)。
奖励(Reward): 每个动作执行后,智能体会收到一个奖励信号,表示该动作的好坏程度。奖励是智能体学习的驱动力,其目标是最大化累积奖励。
智能体的目标是通过学习从状态到动作的映射,即策略,以最大化期望累积奖励。这个学习过程可以通过不同的强化学习算法来实现,如Q学习、深度Q网络(DQN)、策略梯度方法等。
总之,状态描述了环境的当前情况,动作是智能体对当前状态的响应,而奖励是系统提供的反馈,用于指导智能体学习正确的行为。这三个元素共同构成了强化学习中的核心概念。
policy
在强化学习中,策略(policy)是智能体(agent)在特定状态下选择动作的规则或策略函数。策略定义了从环境的状态到智能体选择的动作的映射。形式上,对于某一状态 (s),策略可以表示为:\(\pi(a|s)\)
其中,(\(\pi\)) 是策略函数,它告诉我们在状态 (s) 下选择动作 (a) 的概率。这可以是一个确定性策略(确定性地选择一个动作)或一个概率性策略(以一定概率选择不同的动作)。
强化学习中的目标是学习一个最优策略,使得智能体在与环境的交互中获得最大的累积奖励。学习最优策略的方法主要有两类:
- 值函数方法(Value Function Methods): 这类方法通过估计每个状态或状态动作对的值来指导策略的更新。值函数可以是状态值函数(V-function)或动作值函数(Q-function)。根据值函数,可以选择使值最大化的动作。
- 直接策略优化方法(Direct Policy Optimization Methods): 这类方法直接对策略进行优化,通过参数化的策略函数来寻找最优的策略。常见的方法包括策略梯度方法,其中通过梯度上升更新策略的参数,使得累积奖励增加。
一些常见的策略表示方式包括:
- 确定性策略: (\(\pi(s) = a\)),即在每个状态下直接选择一个确定的动作。
- 概率性策略: (\(\pi(a|s)\)),即在每个状态下以一定的概率分布选择不同的动作。
- 参数化策略: 使用一组参数化的函数来表示策略,例如神经网络。这种策略可以通过学习参数的方式进行优化。
强化学习中策略的选择对于智能体在环境中的表现至关重要。在学习过程中,智能体通过不断尝试不同的策略,根据奖励信号来更新策略,从而逐渐优化其行为。

reward
在强化学习中,奖励(reward)是环境提供给智能体(agent)的一个信号,用于评估智能体在特定状态下采取特定动作的好坏。奖励是智能体学习和改进其策略的主要驱动力。
奖励的作用是引导智能体朝着在特定环境下取得更好结果的方向学习。智能体的目标通常是最大化累积奖励,而奖励信号则在每个时间步鼓励或惩罚智能体的行为。
强化学习中的奖励具有以下一些重要性质:
- 即时奖励(Immediate Reward): 指的是在智能体执行一个动作后立即获得的奖励。即时奖励有助于智能体快速学习适应环境。
- 延迟奖励(Delayed Reward): 指的是与智能体的动作相对应但不是立即获得的奖励。例如,智能体在迷宫中走了一段路程后才获得奖励。延迟奖励要求智能体具备长期规划和记忆能力。
- 稀疏奖励(Sparse Reward): 指的是在许多状态下,奖励为零或非常小。这可能使得智能体面临挑战,因为它需要在大量无奖励的情况下学会正确的行为。
- 稠密奖励(Dense Reward): 指的是在许多状态下,奖励都有非零值。稠密奖励有助于更频繁地提供反馈,促使智能体更快地调整其策略。
在强化学习任务中,设计有效的奖励结构对于训练稳定、高效的智能体至关重要。合理的奖励设置可以帮助克服挑战,引导智能体学到期望的行为。不同的强化学习问题可能需要不同的奖励设计,以便平衡即时奖励和长期目标,以及稀疏和稠密奖励之间的关系。
state transition
在强化学习中,状态转移(state transition)是指智能体从一个状态转移到另一个状态的过程。状态转移是强化学习中马尔可夫决策过程(Markov Decision Process,MDP)的一部分,其中智能体与环境互动,并根据其采取的动作和环境的反馈来改变状态。
具体而言,状态转移可以通过一个转移概率函数来表示。对于一个离散时间步 (t),状态 (\(s_t\)),和动作 (\(a_t\)),状态转移函数 (P) 给出了下一个状态 (\(s_{t+1}\)) 的概率分布:
\(P(s_{t+1} | s_t, a_t)\)
这个概率分布表示在当前状态 (\(s_t\)) 下,执行动作 (\(a_t\)) 后转移到下一个状态 (\(s_{t+1}\)) 的概率。在马尔可夫决策过程中,状态转移满足马尔可夫性质,即下一个状态的概率只依赖于当前状态和执行的动作。
状态转移概率是强化学习算法中的重要组成部分,因为它影响了智能体对环境的理解和学习。智能体根据状态转移的概率分布来估计在不同状态下采取不同动作的结果,从而选择最优的策略来最大化累积奖励。
在连续状态空间中,状态转移函数可能被替代为状态转移密度函数,通常用概率密度函数来表示状态转移到某个区域的概率。这在连续时间的强化学习问题中很常见。
总的来说,状态转移是描述强化学习问题中智能体与环境之间交互的重要概念,对于智能体的决策和学习过程至关重要。
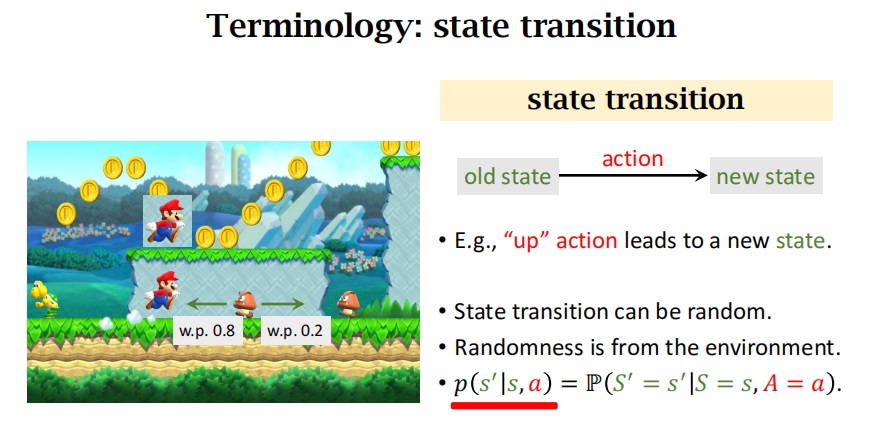
RL中的agent和environment的交互
agent采取行动\(a_{t}\),环境会将状态变成\(s_{t+1}\),并且给一个奖励\(r_{t}\)
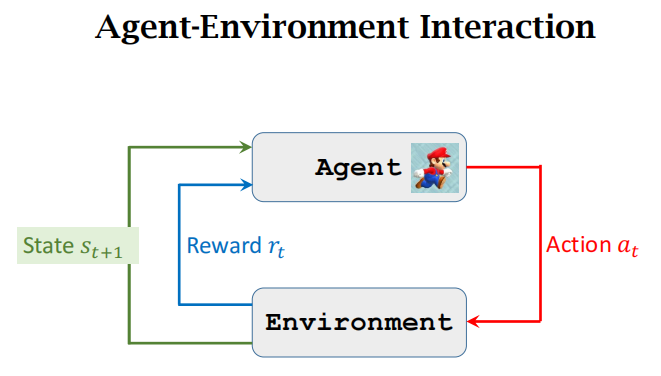
让我们通过《超级马里奥兄弟》(Super Mario Bros.)这个游戏来解释强化学习中的几个重要概念。
- 状态(State): 在《超级马里奥兄弟》中,状态可以是游戏中马里奥所处的具体位置、当前的生命值、关卡的时间等。每一个瞬时的游戏状态都可以被看作一个状态,它描述了游戏的当前情况。
- 动作(Action): 动作是智能体(玩家或马里奥)可以执行的操作,如向左移动、向右跳跃等。在马里奥游戏中,玩家通过按键或操纵杆来执行这些动作,每个动作对应着不同的玩家输入。
- 奖励(Reward): 奖励是智能体根据其动作在特定状态下获得的反馈信号。在《超级马里奥兄弟》中,奖励可以是吃到蘑菇增加生命值,通过管道到达新的区域,或者躲避敌人而保持生命等。获得奖励有助于玩家最终完成关卡。
- 状态转移(State Transition): 状态转移描述了智能体从一个状态到另一个状态的过程。在游戏中,这可以是玩家控制马里奥移动,穿越管道,跳跃到新的平台等。状态转移与玩家的动作和当前状态密切相关。
- 策略(Policy): 在马里奥游戏中,策略是指玩家在特定状态下选择的动作的规则。例如,当马里奥面临一个深坑时,策略可能是选择跳跃以避免掉入坑中。策略可以随着游戏的进行而调整,以最大化累积的奖励。
- 环境(Environment): 游戏环境包括了马里奥、敌人、平台、管道等所有与玩家交互的元素。智能体(玩家)与环境互动,智能体的动作影响环境的状态,并产生奖励信号。
强化学习的目标是学习一个策略,使得在给定状态下选择动作的智能体能够最大化累积奖励,从而高效地完成任务,比如通关关卡。通过理解这些概念,我们可以将强化学习的思想应用于《超级马里奥兄弟》这样的游戏中,以让智能体学会优秀的玩家策略。
两种随机性
- 动作的随机性

- 状态的随机性
环境用状态转移函数算出概率p,然后随机抽样得到下一个状态\(S^{'}\)

这两者的随机性分别来自策略函数和状态转移函数

trajectory
Trajectory(轨迹)在强化学习中指的是智能体(agent)在环境中执行一系列动作的序列,从初始状态开始,通过与环境的交互,经过一系列状态和动作,最终达到终止状态或满足某个结束条件。Trajectory记录了智能体在环境中的轨迹,描述了其行为的历史。
一个典型的强化学习轨迹可以用如下表示:
\((s_0, a_0, r_1, s_1, a_1, r_2, s_2, \ldots, s_{T-1}, a_{T-1}, r_T, s_T)\)
其中:
- (\(s_t\)) 是在时间步 (t) 时的状态(state)。
- (\(a_t\)) 是在时间步 (t) 时智能体选择的动作(action)。
- (\(r_{t+1}\)) 是在执行动作 (\(a_t\)) 后智能体获得的奖励(reward)。
- (\(s_{t+1}\)) 是在执行动作 (\(a_t\))后环境转移到的下一个状态。
- 表示轨迹的结束时刻。
Trajectory包含了智能体与环境的交互历史,对于理解智能体在学习过程中是如何与环境互动的至关重要。在强化学习的许多算法中,学习的目标是通过分析轨迹,优化策略以最大化累积奖励。一些算法如蒙特卡洛方法和时序差分方法都涉及到对轨迹的分析和利用。
轨迹的长度可以因任务的性质而异,可能是有限的,也可能是无限的(例如,在一个连续的控制问题中)。对轨迹的理解有助于研究智能体的行为模式、评估学习算法的性能,并改进智能体的决策策略。
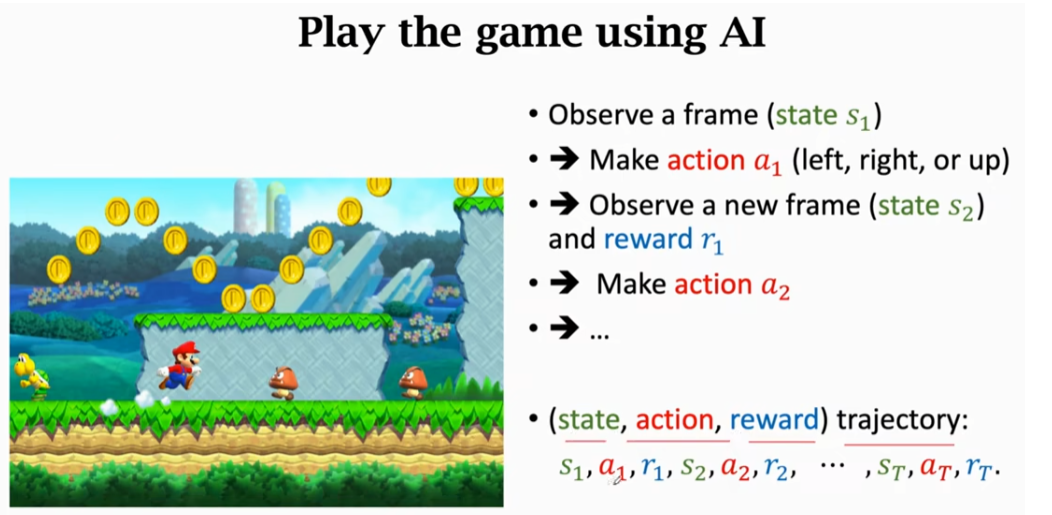
return 和 discounted return
回报(return)是指从当前时刻开始,直到本回合结束的所有奖励的总和,因此回报也被称为累计奖励(cumulative future reward)。将时刻 (t) 的回报表示为随机变量 (\(U_t\))。如果一回合游戏结束,已经观测到所有奖励,那么将回报记作 (\(u_t\))。设本回合在时刻 (n) 结束。定义回报为:
\(U_{t} = R_{t} + R_{t+1} + R_{t+2} + R_{t+3} + \ldots + R_{n}\)
回报的应用主要在于它代表了未来获得的奖励总和,因此智能体的目标是让回报尽量大,即越大越好。强化学习的目标是找到一个策略,使得回报的期望最大化,这个策略被称为最优策略(optimum policy)。
强化学习的目标是最大化回报,而不是最大化当前的奖励。以下棋为例,玩家的目标是赢得一局比赛(回报),而不仅仅是吃掉对方当前的一个棋子(奖励)。
在马尔可夫决策过程(MDP)中,通常使用折扣回报(discounted return),对未来的奖励进行折扣。折扣回报的定义如下:
\(U_{t} = R_{t} + \gamma \cdot R_{t+1} + \gamma^{2} \cdot R_{t+2} + \gamma^{3} \cdot R_{t+3} + \ldots\)
其中,(\(\gamma \in\)[0,1]) 被称为折扣率。对于越久远的未来,奖励打的折扣越大。这种折扣考虑了时间的因素,使得在计算回报时更加关注即时奖励。
return: cumulative future reward

discounted return:cumulative discounted future reward
未来的reward比现在的reward价值低,所以会加一个折扣因子。

return的随机性
discredounted return依赖于\(S_t,{A_t},S_{t+1},{A_{t+1}},\cdots,{S_n},{A_n}.\)即return依赖于从t时刻开始的状态和行动

value functions
action-value function Q(s, a)
在t 时刻,假如我们知道\(U_{t}\)的值,我们就知道游戏是快赢了还是快输了。然而在 t 时刻我们并不知道\(U_{t}\)的值,因为此时\(U_{t}\)仍然是个随机变量。在 t 时刻,我们不知道\(U_{t}\)的值,而我们又想预判\(U_{t}\)的值从而知道局势的好坏。该怎么办呢?解决方案就是对\(U_{t}\)求期望,消除掉其中的随机性。
假设我们已经观测到状态\(s_{t}\),而且做完决策,选中动作\(a_{t}\)。那么\(U_{t}\)中的随机性来自于 t + 1 时刻起的所有的状态和动作:
\(S_{t+1}, A_{t+1}, \quad S_{t+2}, A_{t+2}, \quad \ldots, \quad S_n, A_n.\)
对\(U_t\)关于变量\(S_{t+1},A_{t+1},\cdots,S_n,A_n\)求条件期望,得到
\(Q_{\pi}(s_{t},a_{t})=\mathbb{E}_{S_{t+1},A_{t+1},\cdots,S_{n},A_{n}}\bigg[U_{t}\bigg|S_{t}=s_{t},A_{t}=a_{t}\bigg].\)
期望中的\(S_t=s_t\)和\(A_t=a_t\)是条件,意思是已经观测到\(S_t\)与\(A_t\)的值。条件期望的结果\(Q_\pi(s_t,a_t)\)被称作动作价值函数 (action-value function)。

动作价值函数\(Q_\pi(s_t,a_t)\)依赖于\(s_t\)与\(a_t\), 而不依赖于\(t+1\)时刻及其之后的状态和动作,因为随机变量\(S_{t+1},A_{t+1},\cdots,S_n,A_n\)都被期望消除了。由于动作\(A_{t+1},\cdots,A_n\)的概率质量函数都是\(\pi\),公式中的期望依赖于\(\pi\);用不同的\(\pi\), 求期望得出的结果就会不同。因此\(Q_\pi(s_t,a_t)\)依赖于π, 这就是为什么动作价值函数有下标 π。
综上所述,t时刻的动作价值函数\(Q_\pi(s_t,a_t)\)依赖于以下三个因素:
- 第一,当前状态\(s_t\)。当前状态越好,那么价值\(Q_\pi(s_t,a_t)\)越大,也就是说回报的期望值越大。在超级玛丽的游戏中,如果玛丽奥当前已经接近终点,那么\(Q_\pi(s_t,a_t)\)就非常大。
- 第二,当前动作\(a_t\)。智能体执行的动作越好,那么价值\(Q_\pi(s_t,a_t)\)越大。举个例子, 如果玛丽奥做正常的动作,那么\(Q_\pi(s_t,a_t)\)就比较正常。如果玛丽奥的动作\(a_t\)是跳下悬崖,那么\(Q_\pi(s_t,a_t)\)就会非常小。
- 第三,策略函数π。策略决定未来的动作\(A_{t+1},A_{t+2},\cdots,A_n\)的好坏:策略越好,那么\(Q_\pi(s_t,a_t)\)就越大。举个例子,顶级玩家相当于好的策略 π, 新手相当于差的策略。让顶级玩家操作游戏,回报的期望非常高。换新手操作游戏,从相同的状态出发,回报的期望会很低。
optimal action-value function最优动作价值函数
怎么样才能排除掉策略 π 的影响,只评价当前状态和动作的好坏呢?解决方案就是最优动作价值函数 (optimal action-value function):
\(Q_{\star}(s_{t},a_{t})\:=\:\operatorname*{max}_{\pi}\:Q_{\pi}(s_{t},a_{t}),\quad\forall\:s_{t}\in\mathcal{S},\quad a_{t}\in\mathcal{A}.\)
意思就是有很多种策略函数π可供选择,而我们选择最好的策略函数:
\(\pi^{\star}\:=\:\operatorname*{argmax}_{\pi}\:Q_{\pi}(s_{t},a_{t}),\quad\forall\:s_{t}\in\mathcal{S},\quad a_{t}\in\mathcal{A}.\)
最优动作价值函数\(Q_\star(s_t,a_t)\)只依赖于\(s_t\)和\(a_t\), 而与策略 π 无关。
最优动作价值函数\(Q_{\star}\)非常有用,它就像是一个先知,能指引智能体做出正确决策。比如玩超级玛丽,给定当前状态\(s_t\),智能体该执行动作空间\(\mathcal{A}=\){左,右,上}中的哪个动作呢?假设我们已知\(Q_{\star}\)函数,那么我们就让\(Q_{\star}\)给三个动作打分,比如:
\(Q_{\star}(s_{t},\:\text{左})\:=\:130,\quad Q_{\star}(s_{t},\:\text{右})\:=\:-50,\quad Q_{\star}(s_{t},\:\text{上})\:=\:296.\)
这三个值是什么意思呢?
\(Q_\star ( s_t, 左) = 130\)的意思是:如果现在智能体选择向左走,那么不管以后智能体用什么策略函数π, 回报\(U_t\)的期望最多不会超过130。同理,如果现在向右走,则回报的期望最多不超过 -50。如果现在向上跳,则回报的期望最多不超过296。
智能体应该执行哪个动作呢?毫无疑问,智能体当然应该向上跳,这样才能有希望获得尽量高的回报。
state-value funciton 状态价值函数
假设 AI 用策略函数 π 下围棋。AI 想知道当前状态\(s_t\)(即棋盘上的格局) 是否对自已有利,以及自己和对手的胜算各有多大。该用什么来量化双方的胜算呢?答案是状态价值函数 (state-value function):
\(V_{\pi}(s_{t}) = \mathbb{E}_{A_{t} \sim \pi(\cdot \mid s_{t})} \left[ Q_{\pi}(s_{t}, A_{t}) \right] \\= \sum_{a \in A} \pi(a \mid s_{t}) \cdot Q_{\pi}(s_{t}, a).\)
公式里把动作\(A_t\)作为随机变量,然后关于\(A_t\)求期望,把\(A_t\)消掉。得到的状态价值函数\(V_\pi(s_t)\)只依赖于策略 π 与当前状态\(s_t\), 不依赖于动作。
状态价值函数\(V_{\pi}(s_t)\)也是回报\(U_t\)的期望:
\(V_\pi(s_t)~=~\mathbb{E}_{A_t,S_{t+1},A_{t+1},\cdots,S_n,A_n}\left[U_t\Big|S_t=s_t\right].\)
期望消掉了\(U_t\)依赖的随机变量\(A_t,S_{t+1},A_{t+1},\cdots,S_n,A_n\)。状态价值越大,就意味着回报的期望越大。用状态价值可以衡量策略π与状态\(s_t\)的好坏。

上面的期望计算:对所有可能的动作按照策略 π 的概率进行加权求和
Understanding the Value Functions
- Action-value function:\(Q_\pi(s,\color{red}{a})=\mathbb{E}\left[U_t|S_t=s,\color{red}{A_t=a}\right].\)
- Given policy π ,\(Q_{\pi}(s,\color{red}{\alpha})\)evaluates how good it is for an agent to pick action\(\color{blue}{a}\)while being in state s.
- State-value function:\(V_{\pi}(s)=\mathbb{E}_{\color{red}{A}}\left[Q_{\pi}(s,A)\right]\)
- For fixed policy π ,\(V_{\pi}(s)\)evaluates how good the situation is in state s. +\(\mathbb{E}_S[V_\pi(S)]\)evaluates how good the policy π is.
AI如何控制agent?
两种方法:
policy-based RL 和 value-based RL

Policy-based Reinforcement Learning(基于策略的强化学习)和 Value-based Reinforcement Learning(基于值的强化学习)是强化学习中两种主要的方法,它们在解决问题的策略和价值函数的表示上有所不同。
Policy-based RL (基于策略的强化学习):
特点:
- 直接学习最优策略,而不是通过价值函数间接得到。
- 策略通常表示为一个参数化的概率分布,例如高斯分布。
- 直接优化策略参数以最大化累积奖励。
- 在连续动作空间和高维状态空间中表现良好,适用于非确定性策略。
优势:
- 可以处理高度非线性和连续动作空间。
- 收敛性更好,特别适用于大规模、高维度的问题。
缺点:
- 训练通常更为计算密集。
- 对样本效率要求较高。
Value-based RL (基于值的强化学习):
特点:
- 通过价值函数(通常是状态值函数或动作值函数)来评估动作或状态的好坏。
- 通常使用贝尔曼方程来更新价值函数。
- 通过最优值函数来选择最优动作。
优势:
- 通常更为稳定,对样本效率的要求较低。
- 在有限状态、离散动作的问题中表现良好。
缺点:
- 对于连续动作空间和高维状态空间的处理可能不够灵活。
- 可能会收敛到局部最优解,特别是在非线性问题上。
共同点:
- 目标是学习一个在不同状态或状态-动作对上的策略,以最大化累积奖励。
- 两者都依赖于策略评估和改进的迭代过程。
结论:
- 选择基于策略的方法还是基于值的方法通常取决于具体问题的性质和对问题的建模方式。在实际应用中,有时会结合两者,使用Actor-Critic等混合方法,以发挥它们的优势并弥补彼此的不足。
summary
