1.2 value based RL

复习

1. 在学习DQN之前，首先复习一些基础知识。在一局游戏中，把从起始到结束的所有奖励记作：\(R_1, \cdots, R_t, \cdots, R_n\)。
2. 定义折扣率\(\gamma \in [0, 1]\)。折扣回报的定义是：

\(U_t = R_t + \gamma \cdot R_{t+1} + \gamma^2 \cdot R_{t+2} + \cdots + \gamma^{n-t} \cdot R_n\)。

3. 在游戏尚未结束的\(t\)时刻，\(U_t\)是一个未知的随机变量，其随机性来自于\(t\)时刻之后的所有状态与动作。动作价值函数 的定义是：

\(Q_{\pi}(s_t, a_t) = \mathbb{E}[U_t | S_t = s_t, A_t = a_t]\),

• 公式中的期望消除了t tt 时刻之后的所有状态\(S_{t+1},\cdots,S_n\)与所有动作\(A_{t+1},\cdots,A_n\)

4. 最优动作价值函数用最大化消除策略\(\pi\)：\(Q^*(s_t, a_t) = \max_{\pi} Q_{\pi}(s_t, a_t), \forall s_t \in \mathcal{S}, a_t \in \mathcal{A}\)。
5. 可以这样理解\(Q^*\): 已知\(s_t\)和\(a_t\), 不论未来采取什么样的策略\(\pi\), 回报\(U_t\)的期望不可能超过\(Q^*\)。
6. 最优动作价值函数的用途：假如我们知道\(Q^*\), 我们就能用它做控制。
   1. 举个例子，超级玛丽游戏中的动作空间是\(A = \{左，右，上\}\)。
   2. 给定当前状态\(s_t\), 智能体该执行哪个动作呢？
   3. 假设我们已知\(Q^*\)函数，那么我们就让\(Q^*\)给三个动作打分，
   4. 比如：\(Q^*(s_t, 左) = 370, Q^*(s_t, 右) = -21, Q^*(s_t, 上) = 610\)。
7. 这三个值是什么意思呢？ 1.\(Q^*(s_t, 左) = 370\)的意思是：如果现在智能体选择向左走，不论之后采取什么策略\(\pi\), 那么回报\(U_t\)的期望最多不会超过 370。
   2. 同理，其他两个最优动作价值也是回报的期望的上界。
   3. 根据\(Q^*\)的评分，智能体应该选择向上跳，因为这样可以最大化回报\(U_t\)的期望。

DQN

• 我们希望知道\(Q^*\), 因为它就像是先知一般，可以预见未来，在\(t\)时刻就预见\(t\)到\(n\)时刻之间的累计奖励的期望。
• 假如我们有\(Q^*\)这位先知，我们就遵照先知的指导，最大化未来的累计奖励。
• 然而在实践中我们不知道\(Q^*\)的函数表达式。是否有可能近似出\(Q^*\)这位先知呢？
• 对于超级玛丽这样的游戏，学出来一个“先知”并不难。假如让我们重复玩超级玛丽一亿次，那我们就会像先知一样，看到当前状态，就能准确判断出当前最优的动作是什么。
• 这说明只要有足够多的“经验”, 就能训练出超级玛丽中的“先知”。

1. 最优动作价值函数的近似：
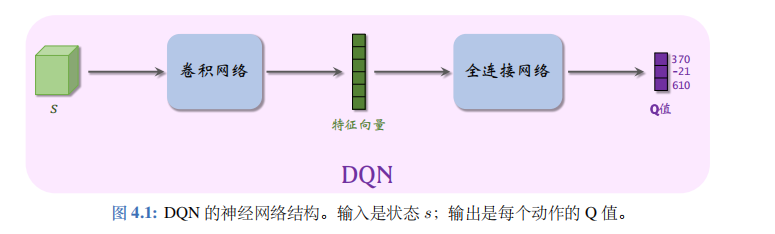
   1. 在实践中，近似学习“先知”\(Q^*\)最有效的办法是深度Q网络(deep Q network, 缩写 DQN), 记作\(Q(s, a; \boldsymbol{w})\), 其结构如图所述。
   2. 其中的\(\boldsymbol{w}\)表示神经网络中的参数。首先随机初始化\(\boldsymbol{w}\), 随后用“经验”去学习\(\boldsymbol{w}\)。
   3. 学习的目标是：对于所有的\(s\)和\(a\), DQN 的预测\(Q(s, a; \boldsymbol{w})\)尽量接近\(Q^*(s, a)\)。后面几节的内容都是如何学习\(\boldsymbol{w}\)!

2. 可以这样理解 DQN 的表达式\(Q(s, a; \boldsymbol{w})\)。
   1. DQN 的输出是离散动作空间\(A\)上的每个动作的 Q 值，即给每个动作的评分，分数越高意味着动作越好。
   2. 举个例子，动作空间是\(A = \{左，右，上\}\), 那么动作空间的大小等于\(|A| = 3\), 那么 DQN 的输出是 3 维的向量，记作\(\hat{q}\), 向量每个元素对应一个动作。
   3. 在图 4.1 中，DQN 的输出是 4.\(q^1 = Q(s, 左; \boldsymbol{w}) = 370, q^2 = Q(s, 右; \boldsymbol{w}) = -21, q^3 = Q(s, 上; \boldsymbol{w}) = 610\)。
3. 总结一下，DQN 的输出是\(|A|\)维的向量\(\hat{q}\), 包含所有动作的价值。而我们常用的符号\(Q(s, a; \boldsymbol{w})\)是标量，是动作\(a\)对应的动作价值，是向量\(\hat{q}\)中的一个元素。
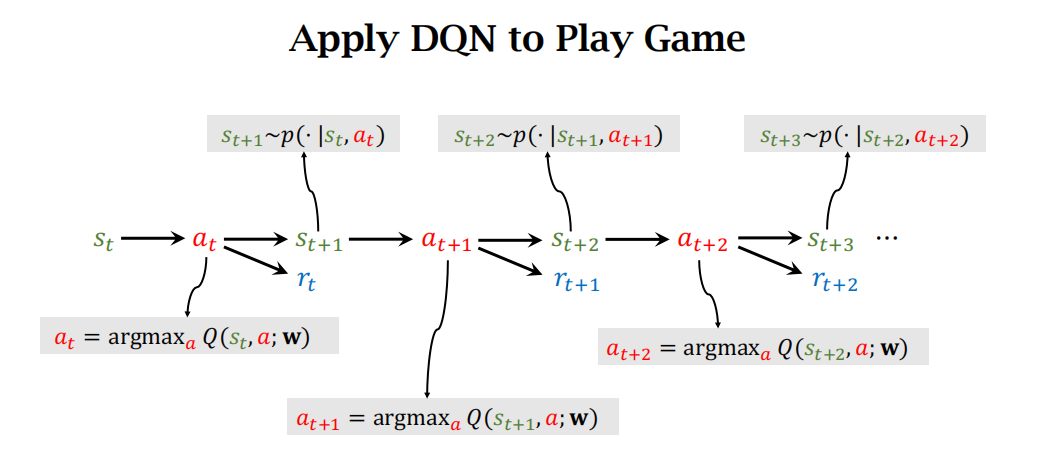
4. 用DQN玩游戏：agent每次采取的action是使得Q函数取最大的那个动作，一直玩下去。下图的顺序是从左往右看。

5. DQN 的梯度：在训练 DQN 的时候，需要对 DQN 关于神经网络参数\(\boldsymbol{w}\)求梯度。用\(\nabla_{w} Q(s, a; w) \triangleq \frac{\partial Q(s, a; w)}{\partial w}\)

• 表示函数值\(Q(s, a; \boldsymbol{w})\)关于参数\(\boldsymbol{w}\)的梯度。因为函数值\(Q(s, a; \boldsymbol{w})\)是一个实数，所以梯度的形状与\(\boldsymbol{w}\)完全相同。
• 如果\(\boldsymbol{w}\)是\(d \times 1\)的向量，那么梯度也是\(d \times 1\)的向量。如果\(\boldsymbol{w}\)是\(d_1 \times d_2\)的矩阵，那么梯度也是\(d_1 \times d_2\)的矩阵。如果\(\boldsymbol{w}\)是\(d_1 \times d_2 \times d_3\)的张量，那么梯度也是\(d_1 \times d_2 \times d_3\)的张量。

6. 给定观测值\(s\)和\(a\), 比如\(a = 左\), 可以用反向传播计算出梯度\(\nabla_{\boldsymbol{w}}Q( s, 左; \boldsymbol{w})\)。
   1. 在编程实现的时候，TensorFlow 和PyTorch 可以对 DQN 输出向量的一个元素(比如\(Q( s, 左; \boldsymbol{w})\)这个元素) 关于变量\(\boldsymbol{w}\)自动求梯度，得到的梯度的形状与\(\boldsymbol{w}\)完全相同。

时间差分（TD）算法

驾车时间预测的例子

1. 假设我们有一个模型\(Q(s, d; \boldsymbol{w})\), 其中\(s\)是起点，\(d\)是终点，\(\boldsymbol{w}\)是参数。
   1. 模型\(Q\)可以预测开车出行的时间开销。
   2. 这个模型一开始不准确，甚至是纯随机的。
   3. 但是随着很多人用这个模型，得到更多数据、更多训练，这个模型就会越来越准，会像谷歌地图一样准。
2. 我们该如何训练这个模型呢？
   1. 在用户出发前，用户告诉模型起点\(s\)和终点\(d\), 模型做一个预测\(\hat{q} = Q(s, d; \boldsymbol{w})\)。
   2. 当用户结束行程的时候，把实际驾车时间\(y\)反馈给模型。
   3. 两者之差\(\hat{q} - y\)反映出模型是高估还是低估了驾驶时间，以此来修正模型，使得模型的估计更准确。
3. 假设我是个用户，我要从北京驾车去上海。从北京出发之前，我让模型做预测，模型告诉我总车程是 14 小时：

\(\hat{q} \triangleq Q(“北京”, “上海”; \boldsymbol{w}) = 14\)。

4. 当我到达上海，我知道自己花的实际时间是 16 小时，并将结果反馈给模型；见图 4.2。

5. 可以用梯度下降对模型做一次更新，具体做法如下。把我的这次旅程作为一组训练数据：

\(s = “北京”, d = “上海”, \hat{q} = 14, y = 16\)。

6. 我们希望估计值\(\hat{q} = Q(s, d; \boldsymbol{w})\)尽量接近真实观测到的\(y\), 所以用两者差的平方作为损失函数：

\(L(\boldsymbol{w}) = \frac{1}{2} [Q(s, d; \boldsymbol{w}) - y]^2\)。

7. 用链式法则计算损失函数的梯度，得到：

\(\nabla_{\boldsymbol{w}}L(\boldsymbol{w}) = (\hat{q} - y) \cdot \nabla_{\boldsymbol{w}}Q(s, d; \boldsymbol{w})\)。

8. 然后做一次梯度下降更新模型参数\(\boldsymbol{w}\)：

\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \nabla_{\boldsymbol{w}}L(\boldsymbol{w})\)，

• 此处的\(\alpha\)是学习率，需要手动调整。在完成一次梯度下降之后，如果再让模型做一次预测，那么模型的预测值

\(Q("北京", "上海"; \boldsymbol{w})\)

• 会比原先更接近\(y = 16\)。

TD算法

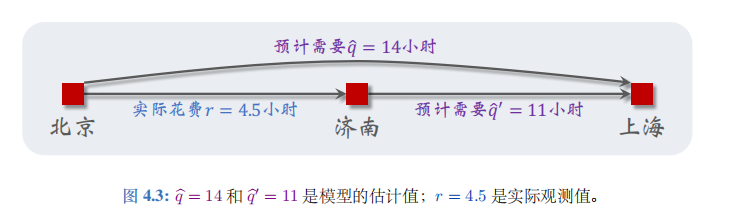
• 接着上文驾车时间的例子。出发前模型估计全程时间为\(\hat{q} = 14\)小时；模型建议的路线会途径济南。我从北京出发，过了\(r = 4.5\)小时，我到达济南。此时我再让模型做一次预测，模型告诉我

\(\hat{q}' \triangleq Q("济南", "上海"; \boldsymbol{w}) = 11\)。

• 见图 4.3 的描述。假如此时我的车坏了，必须要在济南修理，我不得不取消此次行程。
  • 我没有完成旅途，那么我的这组数据是否能帮助训练模型呢？
  • 其实是可以的，用到的算法叫做 时间差分 (temporal difference, 缩写 TD)。

• 下面解释 TD 算法的原理。
  • 回顾一下我们已有的数据：模型估计从北京到上海一共需要\(\hat{q} = 14\)小时，我实际用了\(r = 4.5\)小时到达济南，模型估计还需要\(\tilde{q}' = 11\)小时从济南到上海。
  • 到达济南时，根据模型最新估计，整个旅程的总时间为：
    \(\hat{y} \triangleq r + \hat{q}' = 4.5 + 11 = 15.5\)。
• TD 算法将\(\hat{y} = 15.5\)称为 TD 目标 (TD target), 它比最初的预测\(\hat{q} = 14\)更可靠。
  • 最初的预测\(\hat{q} = 14\)纯粹是估计的，没有任何事实的成分。
  • TD 目标\(\hat{y} = 15.5\)也是个估计，但其中有事实的成分：其中的\(r = 4.5\)就是实际的观测。
• 基于以上讨论，我们认为 TD 目标\(\hat{y} = 15.5\)比模型最初的估计值\(Q(“北京”, “上海”; \boldsymbol{w}) = 14\)更可靠，所以可以用\(\hat{y}\)对模型做“修正”。
  • 我们希望估计值\(\hat{q} = Q(s, d; \boldsymbol{w})\)尽量接近 TD 目标\(\hat{y}\), 所以用两者差的平方作为损失函数：
    \(L(\boldsymbol{w}) = \frac{1}{2} [Q(“北京”, “上海”; \boldsymbol{w}) - \hat{y}]^2\)。
• 此处把\(\hat{y}\)看做常数，尽管它依赖于\(\boldsymbol{w}\)。计算损失函数的梯度：

\(\nabla_{\boldsymbol{w}}L(\boldsymbol{w}) = (\hat{q} - \hat{y}) \cdot \nabla_{\boldsymbol{w}}Q(“北京”, “上海”; \boldsymbol{w})\)，

• 此处的\(\delta = \hat{q} - \hat{y} = 14 - 15.5 = -1.5\)称作 TD 误差 (TD error)。做一次梯度下降更新模型参数\(\boldsymbol{w}\)：
  \(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \delta \cdot \nabla_{\boldsymbol{w}}Q(“北京”, “上海”; \boldsymbol{w})\)。
• 如果你仍然不理解 TD 算法，那么请换个角度来思考问题。模型估计从北京到上海全程需要\(\hat{q} = 14\)小时，模型还估计从济南到上海需要\(\vec{q}' = 11\)小时。这就相当于模型做了这样的估计：从北京到济南需要的时间为\(\hat{q} - \hat{q}' = 14 - 11 = 3\)。
• 而我真实花费\(r = 4.5\)小时从北京到济南。模型的估计与我的真实观测之差为\(\delta = 3 - 4.5 = -1.5\)。这就是 TD 误差！以上分析说明 TD 误差\(\delta\)就是模型估计与真实观测之差。TD 算法的目的是通过更新参数\(\boldsymbol{w}\)使得损失\(L(\boldsymbol{w}) = \frac{1}{2} \delta^2\)减小。

用TD训练DQN

• TD算法是一种在线学习算法，可以逐步更新值函数，而不需要等到回合结束。
• 视频中用到的例子是从纽约到亚特兰大，途径华盛顿，但是道理都是一样的。

• 如何把TD算法用到DQN？和驾车的例子很像，等式左边是 t 时刻的 Q 的估计，等式右边是一个实际观测值加一项关于 t+1 时刻的 Q 估计。

1. 等式\(U_t = R_t + \gamma \cdot U_{t+1}\)

• 这个等式反映了相邻两个折扣回报之间的关系：t 时刻的折扣回报\(U_t\)等于 t 时刻的奖励\(R_t\)加上折扣因子\(\gamma\)乘以 t+1 时刻的折扣回报\(U_{t+1}\)。

2. 得来的过程如下：

\(Q(s_t, a_t; \mathbf{w}) \approx \mathbb{E}[R_t + \gamma \cdot Q(S_{t+1}, A_{t+1}; \mathbf{w})]\)。这个公式两边是两个估计（estimate）

3. 左边是 prediction，右边是 TD target。

4. 使用TD算法训练DQN的过程如下图：下图中的 t+1 时刻的 Q 为什么可以写成 max 的形式？是因为 t+1 时刻的 action\(a_{t+1}\)就是选择 t 时刻使得 Q 最大的那个 action。

5. 下面是王树森书中具体的推导过程：

• 下面我们推导训练 DQN 的 TD 算法（严格地讲，此处推导的是“Q 学习算法”, 它属于 TD 算法的一种。本节就称其为 TD 算法）。回忆一下回报的定义\(U_t = \sum_{k=t}^n \gamma^{k-t} \cdot R_k\),\(U_{t+1} = \sum_{k=t+1}^n \gamma^{k-t-1} \cdot R_k\)。由\(U_t\)和\(U_{t+1}\)的定义可得：

\(U_t = R_t + \gamma \cdot \sum_{k=t+1}^n \gamma^{k-t-1} \cdot R_k = U_{t+1}\)。

• 回忆一下，最优动作价值函数可以写成

\(Q^*(s_t, a_t) = \max_{\pi} \mathbb{E} [U_t | S_t = s_t, A_t = a_t]\)。

• 从公式出发，经过一系列数学推导 , 可以得到下面的定理。这个定理是最优贝尔曼方程 (optimal Bellman equations) 的一种形式。

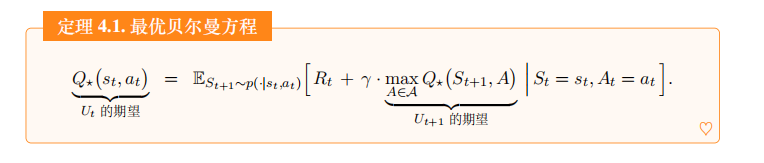
• 最优贝尔曼方程具体公式如下：

\(Q^*(s_t, a_t) = \mathbb{E}{S{t+1} \sim p(\cdot | s_t, a_t)} [R_t + \gamma \cdot \max_{A \in \mathcal{A}} Q^*(S_{t+1}, A) | S_t = s_t, A_t = a_t]\)。

• 贝尔曼方程的右边是个期望，我们可以对期望做蒙特卡洛近似。
  • 当智能体执行动作\(a_t\)之后，环境通过状态转移函数\(p(s_{t+1} | s_t, a_t)\)计算出新状态\(s_{t+1}\)。奖励\(R_t\)最多只依赖于\(S_t\),\(A_t\),\(S_{t+1}\)。那么当我们观测到\(s_t\),\(a_t\),\(s_{t+1}\)时，则奖励\(R_t\)也被观测到，记作\(r_t\)。有了四元组\((s_t, a_t, r_t, s_{t+1})\),
  • 我们可以计算出

\(r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q^*(s_{t+1}, a)\)。

• 它可以看做是下面这项期望的蒙特卡洛近似：

\(\mathbb{E}_{S_{t+1} \sim p(\cdot | s_t, a_t)} [R_t + \gamma \cdot \max_{A \in \mathcal{A}} Q^*(S_{t+1}, A) | S_t = s_t, A_t = a_t]\)。

• 由定理和上述的蒙特卡洛近似可得：

\(Q^*(s_t, a_t) \approx r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q^*(s_{t+1}, a)\)。

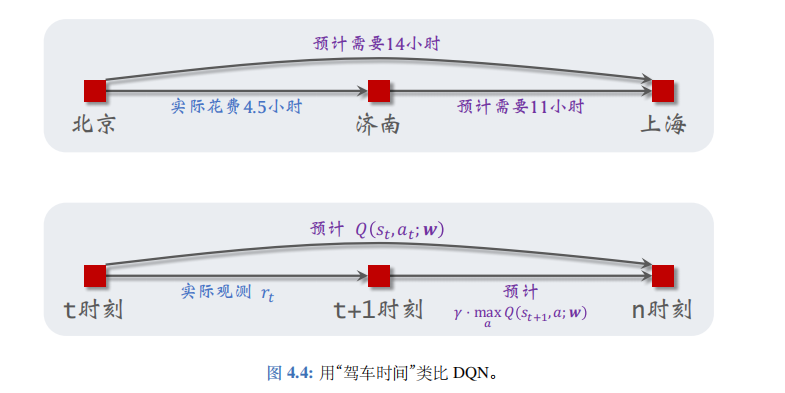
• 这是不是很像驾驶时间预测问题？左边的\(Q^*(s_t, a_t)\)就像是模型预测“北京到上海”的总时间，\(r_t\)像是实际观测的“北京到济南”的时间，\(\gamma \cdot \max_{a \in \mathcal{A}} Q^*(s_{t+1}, a)\)相当于模型预测剩余路程“济南到上海”的时间。见图 4.4 中的类比。

6. 把公式中的最优动作价值函数\(Q^*(s, a)\)替换成神经网络\(Q(s, a; \boldsymbol{w})\), 得到：
   \(Q(s_t, a_t; \boldsymbol{w}) \approx r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q(s_{t+1}, a; \boldsymbol{w})\)。

• 左边的\(\hat{q}_t \triangleq Q(s_t, a_t; \boldsymbol{w})\)是神经网络在 t 时刻做出的预测，其中没有任何事实成分。右边的 TD 目标\(\hat{y}_t\)是神经网络在 t+1 时刻做出的预测，它部分基于真实观测到的奖励\(r_t\)。 +\(\hat{q}_t\)和\(\hat{y}_t\)两者都是对最优动作价值\(Q^*(s_t, a_t)\)的估计，但是\(\hat{y}_t\)部分基于事实，因此比\(\hat{q}_t\)更可信。应当鼓励\(\hat{q}_t \triangleq Q(s_t, a_t; \boldsymbol{w})\)接近\(\hat{y}_t\)。定义损失函数：

\(L(\boldsymbol{w}) = \frac{1}{2} [Q(s_t, a_t; \boldsymbol{w}) - \hat{y}_t]^2\)。

• 假装\(\hat{y}_t\)是常数（实际上\(\hat{y}_t\)依赖于\(\boldsymbol{w}\), 但是我们假装\(\hat{y}_t\)是常数）, 计算\(L\)关于\(\boldsymbol{w}\)的梯度：
  \(\nabla_{\boldsymbol{w}}L(\boldsymbol{w}) = (\hat{q}_t - \hat{y}_t) \cdot \nabla_{\boldsymbol{w}}Q(s_t, a_t; \boldsymbol{w})\)。
• 做一步梯度下降，可以让\(\hat{q}_t\)更接近\(\hat{y}_t\)：
  \(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}}Q(s_t, a_t; \boldsymbol{w})\)。
• 这个公式就是训练 DQN 的 TD 算法。
• 总结一下：最优行动价值函数是未知的，DQN算法就是用神经网络近似这个最优行动价值函数。

7. TD算法具体流程如下：

8. 书中介绍的训练流程

• 首先总结上面的结论。给定一个四元组\((s_t, a_t, r_t, s_{t+1})\), 我们可以计算出 DQN 的预测值\(\hat{q}_t = Q(s_t, a_t; \boldsymbol{w})\), 以及 TD 目标和 TD 误差：
  \(\hat{y}_t = r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q(s_{t+1}, a; \boldsymbol{w})\)和\(\delta_t = \hat{q}_t - \hat{y}_t\)。
• TD 算法用这个公式更新 DQN 的参数：
  \(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}}Q(s_t, a_t; \boldsymbol{w})\)。
• 注意，算法所需数据为四元组\((s_t, a_t, r_t, s_{t+1})\), 与控制智能体运动的策略\(\pi\)无关。这就意味着可以用任何策略控制智能体与环境交互，同时记录下算法运动轨迹，作为训练数据。因此，DQN 的训练可以分割成两个独立的部分：收集训练数据、更新参数\(\boldsymbol{w}\)。

9. 收集训练数据：

• 我们可以用任何策略函数\(\pi\)去控制智能体与环境交互，这个\(\pi\)就叫做行为策略 (behavior policy)。比较常用的是\(\epsilon\)-greedy 策略：
  \(a_t = \left\{ \begin{array}{ll} \arg\max_a Q(s_t, a; \boldsymbol{w}), & \text{以概率 } (1 - \epsilon); \\ \text{均匀抽取 } A \text{ 中的一个动作}, & \text{以概率 } \epsilon. \end{array} \right.\)
• 把智能体在一局游戏中的轨迹记作：
  \(s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_n, a_n, r_n\)。
• 把一条轨迹划分成\(n\)个\((s_t, a_t, r_t, s_{t+1})\)这种四元组，存入数组，这个数组叫做经验回放数组 (replay buffer)。

10. 更新 DQN 参数\(\boldsymbol{w}\)：

• 随机从经验回放数组中取出一个四元组，记作\((s_j, a_j, r_j, s_{j+1})\)。
• 设 DQN 当前的参数为\(\boldsymbol{w}_{\text{now}}\), 执行下面的步骤对参数做一次更新，得到新的参数\(\boldsymbol{w}_{\text{new}}\)。
  1. 对 DQN 做正向传播，得到 Q 值：
     \(\hat{q}_j = Q(s_j, a_j; \boldsymbol{w}_{\text{now}})\)和\(\hat{q}_{j+1} = \max_{a \in \mathcal{A}} Q(s_{j+1}, a; \boldsymbol{w}_{\text{now}})\)。
  2. 计算 TD 目标和 TD 误差：
     \(\hat{y}_j = r_j + \gamma \cdot \hat{q}_{j+1}\)和\(\delta_j = \hat{q}_j - \hat{y}_j\)。
  3. 对 DQN 做反向传播，得到梯度：
     \(\boldsymbol{g}_j = \nabla_{\boldsymbol{w}} Q(s_j, a_j; \boldsymbol{w}_{\text{now}})\)。
  4. 做梯度下降更新 DQN 的参数：
     \(\boldsymbol{w}_{\text{new}} \leftarrow \boldsymbol{w}_{\text{now}} - \alpha \cdot \delta_j \cdot \boldsymbol{g}_j\)。

智能体收集数据、更新 DQN 参数这两者可以同时进行。可以在智能体每执行一个动作之后，对\(\boldsymbol{w}\)做几次更新。也可以在每完成一局游戏之后，对 \(\boldsymbol{w}\) 做几次更新。

注意

上面介绍用 TD 算法训练 DQN, 更准确地说，我们用的 TD 算法叫做 Q 学习算法 (Q-learning)。TD 算法是一大类算法，常见的有 Q 学习和 SARSA。Q 学习的目的是学到最优动作价值函数 \(Q^*\), 而 SARSA 的目的是学习动作价值函数 \(Q_{\pi}\)。后面会介绍 SARSA 算法。