1.3 策略学习

复习策略函数

1. 复习策略函数的定义：策略函数是一个概率密度函数，把state作为输入，输出一个所有action的概率分布。

策略网络policy network

用神经网络来近似策略函数\(\pi\)。

状态价值函数回顾

1. 状态价值函数是对动作价值函数求期望（关于action积分（或累加和），将action消掉）。

2. 近似状态价值函数：用策略网络近似策略函数，然后将其带入价值函数中，如下图所示。主要的区别是里面多了一个\(\theta\)变量，这是神经网络的参数。

3. 改进模型参数\(\theta\)使得V函数变大，目标函数\(J(\theta)\)是对V函数求期望，J函数是对策略网络的评价，策略网络越好，J就越大。
4. policy based learning的目标就是改进模型参数\(\theta\)使得\(J(\theta)\)越大越好。

策略梯度policy gradient

1. 推导策略梯度

2. 下面用了log函数求导的性质，从第一个蓝色方框推到到第二个蓝色方框。

• 第二个等式关于\(\pi\)求和，就是对随机变量A求期望。

• 经过推导，得到策略梯度下面两种形式

3. 对于离散动作求策略梯度：用form1

4. 对于连续动作求策略梯度：用form2，这里用到了蒙特卡洛近似

Update policy network using policy gradient

• 策略梯度算法：每一轮迭代都做如下的6步

• 对于第三步\(q_t \approx Q_{\pi}(s_t, a_t)\)中的动作价值函数\(Q_{\pi}\)不知道是什么，有两个办法近似计算\(q_t\)
  • 第一个算法：REINFORCE算法
    • 如下图所示：但是它需要玩完一轮游戏，观测到所有的奖励，然后才能更新策略网络。
    
• 第二个方法：用神经网络代替\(Q_{\pi}\)

• 总结一下：如果策略函数已知，那么agent的动作就可以采样这个策略函数，进而被控制。但是策略函数不知道，所以用策略网络来近似这个策略函数。
• 具体是用策略梯度算法来学习策略网络。

书

• 策略学习(policy-based reinforcement learning) 以及策略梯度 (policy gradient)。策略学习的意思是通过求解一个优化问题，学出最优策略函数或它的近似函数(比如策略网络)。

策略网络

本章假设动作空间是离散的，比如\(A=\{左，右，上\}\)。策略函数\(\pi\)是个条件概率质量函数：

\(\pi(a|s) \triangleq P(A=a|S=s).\)

策略函数\(\pi\)的输入是状态\(s\)和动作\(a\), 输出是一个 0 到 1 之间的概率值。 举个例子，把超级玛丽游戏当前屏幕上的画面作为\(s\), 策略函数会输出每个动作的概率值：

\(\pi(左|s) = 0.5, \quad \pi(右|s) = 0.2, \quad \pi(上|s) = 0.3.\)

如果我们有这样一个策略函数，我们就可以拿它控制 智能体。每当观测到一个状态\(s\),就用策略函数计算出每个动作的概率值，然后做随机抽样，得到一个动作\(a\),让智能体执行\(a\)。

怎么样才能得到这样一个策略函数呢？当前最有效的方法是用神经网络\(\pi(a|s;\theta)\)近似策略函数\(\pi(a|s)\)。神经网络\(\pi(a|s;\theta)\)被称为策略网络。

\(\theta\)表示神经网络的参数；一开始随机初始化\(\theta\),随后利用收集的状态、动作、奖励去更新\(\theta\)。

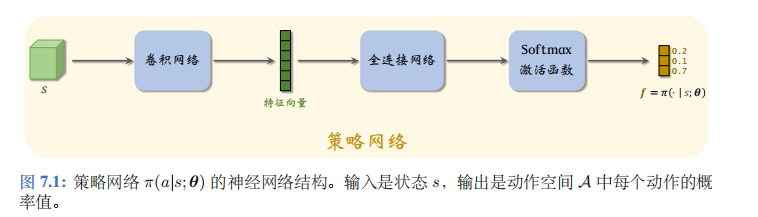
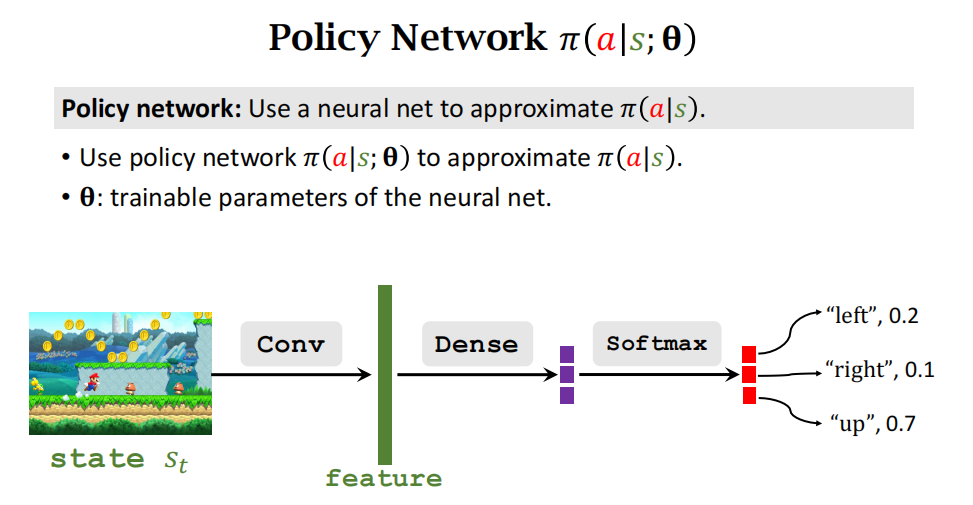
策略网络的结构如图 7.1 所示。策略网络的输入是状态\(s\)。在 Atari 游戏、围棋等应用中，状态是张量 (比如图片),那么应该如图 7.1 所示用卷积网络处理输入。在机器人控制等应用中，状态\(s\)是向量，它的元素是多个传感器的数值，那么应该把卷积网络换成全连接网络。策略网络输出层的激活函数是 softmax, 因此输出的向量 (记作\(f\)) 所有元素都是正数，而且相加等于1。动作空间\(A\)的大小是多少，向量\(f\)的维度就是多少。在超级玛丽的例子中，\(A=\{左，右，上\}\),那么\(f\)就是 3 维的向量，比如\(f = [0.2, 0.1, 0.7]\)。

\(f\)描述了动作空间\(A\)上的离散概率分布，\(f\)每个元素对应一个动作：

\(f_1 = \pi(左|s) = 0.2, \quad f_2 = \pi(右|s) = 0.1, \quad f_3 = \pi(上|s) = 0.7.\)

策略学习的目标函数

为了推导策略学习的目标函数，我们需要先复习回报和价值函数。回报\(U_t\)是从\(t\)时刻开始的所有奖励之和。\(U_t\)依赖于\(t\)时刻开始的所有状态和动作：

\(S_t, A_t, S_{t+1}, A_{t+1}, S_{t+2}, A_{t+2}, \cdots\)

在\(t\)时刻，\(U_t\)是随机变量，它的不确定性来自于未来未知的状态和动作。动作价值函数的定义是：

\(Q_{\pi}(s_t, a_t) = \mathbb{E}[U_t | S_t = s_t, A_t = a_t].\)

条件期望把\(t\)时刻状态\(s_t\)和动作\(a_t\)看做已知观测值，把\(t+1\)时刻后的状态和动作看做未知变量，并消除这些变量。状态价值函数的定义是：

\(V_{\pi}(s_t) = \mathbb{E}_{A_t \sim \pi(\cdot | s_t; \theta)}[Q_{\pi}(s_t, A_t)].\)

状态价值既依赖于当前状态\(s_t\), 也依赖于策略网络\(\pi\)的参数\(\theta\)。

• 当前状态\(s_t\)越好，则\(V_{\pi}(s_t)\)越大，即回报\(U_t\)的期望越大。例如，在超级玛丽游戏中，如果玛丽奥已经接近终点(也就是说当前状态\(s_t\)很好),那么回报的期望就会很大。
• 策略\(\pi\)越好 (即参数\(\theta\)越好),那么\(V_{\pi}(s_t)\)也会越大。例如，从同一起点出发打游戏，高手 (好的策略) 的期望回报远高于初学者 (差的策略)。

如果一个策略很好，那么状态价值\(V_{\pi}(S)\)的均值应当很大。因此我们定义目标函数：

\(J(\theta) = \mathbb{E}_S[V_{\pi}(S)].\)

这个目标函数排除掉了状态\(S\)的因素，只依赖于策略网络\(\pi\)的参数\(\theta\); 策略越好，则\(J(\theta)\)越大。所以策略学习可以描述为这样一个优化问题：

\(\max_{\theta} J(\theta).\)

我们希望通过对策略网络参数\(\theta\)的更新，使得目标函数\(J(\theta)\)越来越大，也就意味着策略网络越来越强。想要求解最大化问题，显然可以用梯度上升更新\(\theta\),使得\(J(\theta)\)增大。设当前策略网络的参数为\(\theta_{\text{now}}\),做梯度上升更新参数，得到新的参数\(\theta_{\text{new}}\):

\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} + \beta \cdot \nabla_{\theta} J(\theta_{\text{now}}).\)

此处的\(\beta\)是学习率，需要手动调整。上面的公式就是训练策略网络的基本思路，其中的梯度

\(\nabla_{\theta} J\left(\theta_{\text{now}}\right) \triangleq \frac{\partial J(\theta)}{\partial \theta} \bigg|_{\theta = \theta_{\text{now}}}\)

被称作策略梯度。策略梯度可以写成下面定理中的期望形式。之后的算法推导都要基于这个定理，并对其中的期望做近似。

\(\frac{\partial J(\theta)}{\partial \theta} = \mathbb{E}_S \left[ \mathbb{E}_{A \sim \pi(\cdot|\theta)} \left[ \frac{\partial \ln \pi(A|S;\theta)}{\partial \theta} \cdot Q_{\pi}(S,A) \right] \right].\)

注 上面的策略梯度定理是不严谨的表述，尽管大多数论文和书籍使用这种表述。严格地讲，这个定理只有在“状态\(S\)服从马尔科夫链的稳态分布\(d(\cdot)\)”这个假设下才成立。定理中的等号其实是不对的，期望前面应该有一项系数\(\frac{1-\gamma^n}{1-\gamma}\),其中\(\gamma\)是折扣率，\(n\)是一局游戏的长度。严格地讲，策略梯度定理应该是：

\(\frac{\partial J(\theta)}{\partial \theta} = \frac{1-\gamma^n}{1-\gamma} \cdot \mathbb{E}_S \sim d(\cdot) \left[ \mathbb{E}_{A \sim \pi(\cdot|S;\theta)} \left[ \frac{\partial \ln \pi(A|S;\theta)}{\partial \theta} \cdot Q_{\pi}(S,A) \right] \right].\)

\(1-\gamma^n\)会被学习率\(\beta\)吸收。

策略梯度定理的证明

把策略网络\(\pi(a|s;\theta)\)看做动作的概率质量函数 (或概率密度函数)。状态价值函数\(V_{\pi}(s)\)可以写成：

\(V_{\pi}(s) = \mathbb{E}_{A \sim \pi(\cdot|\theta)}[Q_{\pi}(s,A)] = \sum_{a \in A} \pi(a|s;\theta) \cdot Q_{\pi}(s,a).\)

状态价值\(V_{\pi}(s)\)关于\(\theta\)的梯度可以写作：

\(\frac{\partial V_{\pi}(s)}{\partial \theta} = \frac{\partial}{\partial \theta} \sum_{a \in A} \pi(a|s;\theta) \cdot Q_{\pi}(s,a) = \sum_{a \in A} \frac{\partial \pi(a|s;\theta) \cdot Q_{\pi}(s,a)}{\partial \theta}\)

上面第二个等式把求导放入连加里面；等式成立的原因是求导的对象\(\theta\)与连加的对象\(u\)不同。回忆一下链式法则：设\(z = f(x) \cdot g(x)\), 那么

\(\frac{\partial z}{\partial x} = \frac{\partial f(x)}{\partial x} \cdot g(x) + f(x) \cdot \frac{\partial g(x)}{\partial x}\).

应用链式法则，公式 (7.1) 中的梯度可以写作：

\(\begin{align*} \frac{\partial V_{\pi}(s)}{\partial \theta} &= \sum_{a \in \mathcal{A}} \frac{\partial \pi(a \mid s; \theta)}{\partial \theta} \cdot Q_{\pi}(s, a) + \sum_{a \in \mathcal{A}} \pi(a \mid s; \theta) \cdot \frac{\partial Q_{\pi}(s, a)}{\partial \theta} \\ &= \sum_{a \in \mathcal{A}} \frac{\partial \pi(a \mid s; \theta)}{\partial \theta} \cdot Q_{\pi}(s, a) + \underbrace{E_{A \sim \pi(\cdot \mid s; \theta)}}_{\text{设为 } x} \left[ \frac{\partial Q_{\pi}(s, A)}{\partial \theta} \right]. \end{align*}\)

上面公式最右边一项\(x\)的分析非常复杂，此处不具体分析了。由上面的公式可得：

\(\begin{align*} \frac{\partial V_{\pi}(s)}{\partial \theta} &= \sum_{A \in \mathcal{A}} \frac{\partial \pi(A \mid S; \theta)}{\partial \theta} \cdot Q_{\pi}(S, A) + x \\ &= \sum_{A \in \mathcal{A}} \pi(A \mid S; \theta) \cdot \frac{1}{\pi(A \mid S; \theta)} \cdot \frac{\partial \pi(A \mid S; \theta)}{\partial \theta} \cdot Q_{\pi}(S, A) + x \\ &= \sum_{A \in \mathcal{A}} \pi(A \mid S; \theta) \cdot \frac{\partial \ln \pi(A \mid S; \theta)}{\partial \theta} \cdot Q_{\pi}(S, A) + x. \end{align*}\)

\(\frac{\partial V_{\pi}(s)}{\partial \theta} = \mathbb{E}_{A \sim \pi(\cdot|\theta)} \left[ \frac{\partial \ln \pi(A|S;\theta)}{\partial \theta} \cdot Q_{\pi}(S,A) \right] + x. \quad (7.2)\)

公式中红色标出的\(\pi(A|S;\theta)\)被看做概率质量函数，因此连加可以写成期望的形式。由目标函数的定义\(J(\theta) = \mathbb{E}_S[V_{\pi}(S)]\)可得：

\(\frac{\partial J(\theta)}{\partial \theta} = \mathbb{E}_S \left[ \frac{\partial V_{\pi}(S)}{\partial \theta} \right] = \mathbb{E}_S \left[ \mathbb{E}_{A \sim \pi(\cdot|\theta)} \left[ \frac{\partial \ln \pi(A|S;\theta)}{\partial \theta} \cdot Q_{\pi}(S,A) \right] \right] + \mathbb{E}_S[x].\)

不严谨的证明通常忽略掉\(x\), 于是得到定理 7.1。

近似策略梯度

先复习一下前两小节的内容。策略学习可以表述为这样一个优化问题：

\(\max_{\theta} \left\{ J(\theta) \triangleq \mathbb{E}_S \left[ V_{\pi}(S) \right] \right\}.\)

求解这个最大化问题最简单的算法就是梯度上升：

\(\theta \leftarrow \theta + \beta \cdot \nabla_{\theta} J(\theta).\)

其中的\(\nabla_{\theta} J(\theta)\)是策略梯度。策略梯度定理证明：

\(\nabla_{\theta} J(\theta) = \mathbb{E}_S \left[ \mathbb{E}_{A \sim \pi(\cdot|\theta)} \left[ Q_{\pi}(S,A) \cdot \nabla_{\theta} \ln \pi(A|S;\theta) \right] \right].\)

解析求出这个期望是不可能的，因为我们并不知道状态\(S\)概率密度函数；即使我们知道\(S\)的概率密度函数，能够通过连加或者定积分求出期望，我们也不愿意这样做，因为连加或者定积分的计算量非常大。

回忆一下，第 2 章介绍了期望的蒙特卡洛近似方法，可以将这种方法用于近似策略梯度。每次从环境中观测到一个状态\(s\), 它相当于随机变量\(S\)的观测值。然后再根据当前的策略网络 (策略网络的参数必须是最新的) 随机抽样得出一个动作：

\(a \sim \pi(\cdot | s; \theta).\)

计算随机梯度：

\(\boldsymbol{g}(s,a;\theta) \triangleq Q_{\pi}(s,a) \cdot \nabla_{\theta} \ln \pi(a|s;\theta).\)

很显然，\(\boldsymbol{g}(s,a;\theta)\)是策略梯度\(\nabla_{\theta} J(\theta)\)的无偏估计：

\(\nabla_{\theta} J(\theta) = \mathbb{E}_S \left[ \mathbb{E}_{A \sim \pi(\cdot|\theta)} \left[ \boldsymbol{g}(S,A;\theta) \right] \right].\)

于是我们得到下面的结论：

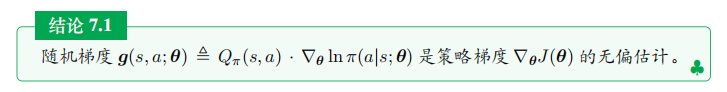
对无偏估计的解释：ChatGPT

在统计学和概率论中，一个估计量如果在多次独立重复采样下的期望值等于被估计的参数的真实值，那么这个估计量被称为 无偏估计。换句话说，无偏估计的期望值与被估计参数的真实值相等，不存在系统性的估计偏差。

形式上，对于估计量 (\(\hat{\theta}\)) 和真实参数 (\(\theta\))，如果满足：

\(\mathbb{E}[\hat{\theta}] = \theta,\)

其中，(\(\mathbb{E}[\cdot]\)) 表示期望值，那么估计量 (\(\hat{\theta}\)) 就是无偏估计。

无偏性是一个重要的性质，因为它意味着在长期的统计学意义上，估计量不会系统性地高估或低估真实参数值。然而，无偏性并不意味着在单次估计中估计值一定会非常接近真实值。方差和均方误差也是评价估计量性能的重要指标。

在实际应用中，研究人员通常希望使用无偏估计，因为它们在统计学理论中更容易处理。但并非所有估计都能找到无偏的形式，有时可能需要权衡无偏性与其他性质（例如方差）来选择合适的估计方法。

应用上述结论，我们可以做随机梯度上升来更新\(\theta\), 使得目标函数\(J(\theta)\)逐渐增长：

\(\theta \leftarrow \theta + \beta \cdot \boldsymbol{g}(s,a;\theta).\)

此处的\(\beta\)是学习率，需要手动调整。但是这种方法仍然不可行，我们计算不出\(\boldsymbol{g}(s,a;\theta)\), 原因在于我们不知道动作价值函数\(Q_{\pi}(s,a)\)。在后面两节中，我们用两种方法对\(Q_{\pi}(s,a)\)做近似：一种方法是 REINFORCE, 用实际观测的回报\(u\)近似\(Q_{\pi}(s,a)\); 另一种方法是actor-critic, 用神经网络\(q(s,a;\boldsymbol{w})\)近似\(Q_{\pi}(s,a)\)。

REINFORCE

策略梯度方法用\(\nabla_{\theta} J(\theta)\)的近似来更新策略网络参数\(\theta\), 从而增大目标函数。上一节中，我们推导出策略梯度\(\nabla_{\theta} J(\theta)\)的无偏估计，即下面的随机梯度：

\(\boldsymbol{g}(s,a;\theta) \triangleq Q_{\pi}(s,a) \cdot \nabla_{\theta} \ln \pi(a|s;\theta).\)

但是其中的动作价值函数\(Q_{\pi}\)是未知的、导致无法直接计算\(\boldsymbol{g}(s,a;\theta)\)。REINFORCE 进一步对\(Q_{\pi}\)做蒙特卡洛近似，把它替换成回报\(u\)。

REINFORCE 的简化推导

设一局游戏有\(n\)步，一局中的奖励记作\(R_1, \cdots, R_n\)。回忆一下，\(t\)时刻的折扣回报定义为：

\(U_t = \sum_{k=t}^n \gamma^{k-t} \cdot R_k.\)

而动作价值定义为\(U_t\)的条件期望：

\(Q_{\pi}(s_t, a_t) = \mathbb{E}[U_t | S_t = s_t, A_t = a_t].\)

我们可以用蒙特卡洛近似上面的条件期望。从时刻\(t\)开始，智能体完成一局游戏，观测到全部奖励\(r_t, \cdots, r_n\), 然后可以计算出\(u_t = \sum_{k=t}^n \gamma^{k-t} \cdot r_k\)。因为\(u_t\)是随机变量\(U_t\)的观测值，所以\(u_t\)是上面公式中期望的蒙特卡洛近似。在实践中，可以用\(u_t\)代替\(Q_{\pi}(s_t, a_t)\), 那么随机梯度\(\boldsymbol{g}(s_t, a_t; \theta)\)可以近似成：

\(\tilde{\boldsymbol{g}}(s_t, a_t; \theta) = u_t \cdot \nabla_{\theta} \ln \pi(a_t | s_t; \theta).\)

\(\tilde{\boldsymbol{g}}\)是\(\boldsymbol{g}\)的无偏估计，所以也是策略梯度\(\nabla_{\theta} J(\theta)\)的无偏估计；\(\tilde{\boldsymbol{g}}\)也是一种随机梯度。

我们可以用反向传播计算出\(\ln \pi\)关于\(\theta\)的梯度，而且可以实际观测到\(u_t\), 于是我们可以实际计算出随机梯度\(\tilde{\boldsymbol{g}}\)的值。有了随机梯度的值，我们可以做随机梯度上升更新策略网络参数\(\theta\):

\(\theta \leftarrow \theta + \beta \cdot \tilde{\boldsymbol{g}}(s_t, a_t; \theta).\)

根据上述推导，我们得到了训练策略网络的算法，即 REINFORCE。

训练流程

当前策略网络的参数是\(\theta_{\text{now}}\)。REINFORCE 执行下面的步骤对策略网络的参数做一次更新：

1. 用策略网络\(\theta_{\text{now}}\)控制智能体从头开始玩一局游戏，得到一条轨迹 (trajectory):\(s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_n, a_n, r_n\).
2. 计算所有的回报：\(u_t = \sum_{k=t}^n \gamma^{k-t} \cdot r_k, \forall t=1, \cdots, n\).
3. 用\(\{(s_t, a_t)\}_{t=1}^n\)作为数据，做反向传播计算：\(\nabla_{\theta} \ln \pi(a_t | s_t; \theta_{\text{now}}), \forall t=1, \cdots, n\).
4. 做随机梯度上升更新策略网络参数：\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} + \beta \cdot \sum_{t=1}^n \gamma^{t-1} \cdot u_t \cdot \nabla_{\theta} \ln \pi(a_t | s_t; \theta_{\text{now}})\).

注：在算法最后一步中，随机梯度前面乘以系数\(\gamma^{t-1}\)。为什么需要这个系数呢？原因是这样的：前面 REINFORCE 的推导是简化的，而非严谨的数学推导；按照我们简化的推导，不应该乘以系数\(\gamma^{t-1}\)。当进行严格的数学推导的时候，得出的 REINFORCE 算法需要系数 \(\gamma^{t-1}\)。

注：REINFORCE 属于同策略 (on-policy), 要求行为策略 (behavior policy) 与目标策略 (target policy) 相同，两者都必须是策略网络 \(\pi(a|s;\theta_{\text{now}})\), 其中 \(\theta_{\text{now}}\) 是策略网络当前的参数。所以经验回放不适用于 REINFORCE。