2.1 蒙特卡洛估计

ChatGPT对蒙特卡洛方法的介绍

蒙特卡洛方法是一类基于随机抽样和统计学原理的数值计算方法，其核心思想是通过随机抽样来近似解决问题。这种方法在强化学习、优化问题、概率估计等领域都有广泛的应用。以下是关于蒙特卡洛方法的一些基本概念：

1. 基本思想
   • 随机抽样： 蒙特卡洛方法利用随机抽样的方式来近似计算某个问题的数值解。通过大量的随机样本，可以得到对问题的概率分布、期望值等进行估计的结果。
2. 应用领域
   • 强化学习： 在强化学习中，蒙特卡洛方法用于估计状态值、动作值，以及计算策略的期望回报。通过采样多条轨迹，可以近似地计算期望值。
   • 数值积分： 蒙特卡洛方法可以用于估计复杂函数的积分值。通过在函数定义域内随机采样，计算函数值的平均值，可以得到积分的近似值。
   • 概率估计： 蒙特卡洛方法在概率估计中也有应用，例如通过采样估计随机变量的期望、方差等统计量。
3. 算法步骤
   1. 随机抽样： 根据问题的特性，通过随机抽样生成一系列样本点。
   2. 计算统计量： 对每个样本点进行计算，得到需要估计的统计量，例如期望值、方差等。
   3. 平均估计： 对所有样本点计算的统计量进行平均，得到最终的近似解。
4. 优缺点
   • 优点： 蒙特卡洛方法是一种通用的数值计算方法，对于复杂问题具有很强的适应性。它不依赖于问题的具体形式，而是通过随机抽样来逼近解。
   • 缺点： 收敛速度相对较慢，特别是在维度较高的问题中，需要大量的样本才能获得准确的估计。同时，对于一些问题，可能存在抽样偏差。

总体而言，蒙特卡洛方法是一种强大的数值计算工具，尤其在面对复杂、高维度的问题时显示出其优越性。

蒙特卡洛(Monte Carlo) 是一大类随机算法(randomized algorithms) 的总称，它们通过随机样本来估算真实值。本节用几个例子讲解蒙特卡洛算法。

例一：近似\(\pi\)值

我们都知道圆周率\(\pi\)约等于 3.1415927。现在假装我们不知道\(\pi\), 而是要想办法近似估算\(\pi\)值。假设我们有一个 (伪) 随机数生成器，我们能不能用随机样本来近似\(\pi\)呢？这一小节讨论使用蒙特卡洛如何近似\(\pi\)值。

假设我们有一个 (伪) 随机数生成器，可以均匀生成 -1 到 +1 之间的数。每次生成两个随机数，一个作为\(x\),另一个作为\(y\)。于是每次生成了一个平面坐标系中的点\((x,y)\), 见图 2.3(左)。因为\(x\)和\(y\)都是在 ([-1,1]) 区间上均匀分布，所以这个正方形内的点被抽到的概率是相同的。我们重复抽样\(n\)次，得到了\(n\)个正方形内的点。

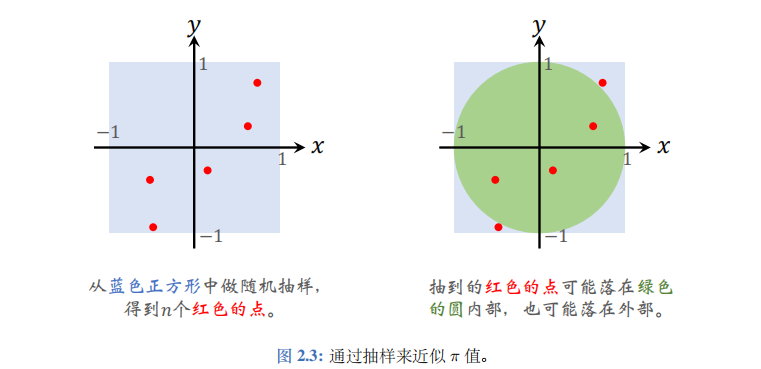
如图2.3(右)所示，蓝色正方形里面包含一个绿色的圆，圆心是(0,0),半径等于1。刚才随机生成的\(n\)个点有些落在圆外面，有些落在圆里面。

请问一个点落在圆里面的概率有多大呢？由于抽样是均匀的，因此这个概率显然是圆的面积与正方形面积的比值。正方形的面积是边长的平方，即\(a_1=2^2=4\)。圆的面积是\(\pi \times 1^2=\pi\)。那么一个点落在圆里面的概率就是\(p=\frac{a_2}{a_1}=\frac{\pi}{4}\)。

设我们随机抽样了\(n\)个点，设圆内的点的数量为随机变量\(M\)。显然，\(M\)的期望等于\(\mathbb{E}[M]=pn=\frac{\pi n}{4}\)。

注意，这只是期望，并不是实际发生的结果。如果你抽\(n=5\)个点，那么期望有\(\mathbb{E}[M]=\frac{5\pi}{4}\)个点落在圆内。但实际观测值\(m\)可能等于 0、1、2、3、4、5 中的任何一个。

给定一个点的坐标\((x,y)\),如何判断该点是否在圆内呢？已知圆心在原点，半径等于1,我们用一下圆的方程。如果\((x,y)\)满足：\(x^2+y^2\leq1\),则说明\((x,y)\)落在圆里面；反之，点就在圆外面。

我们均匀随机抽样得到\(n\)个点，通过圆的方程对每个点做判别，发现有\(m\)个点落在圆里面。如果\(n\)非常大，那么随机变量\(M\)的真实观测值\(m\)就会非常接近期望\(\mathbb{E}[M]=\frac{\pi n}{4}\):

\(m \approx \frac{\pi n}{4}.\)

由此得到：

\(\pi \approx \frac{4m}{n}.\)

我们可以依据这个公式做编程实现。下面是伪代码：

1. 初始化\(m=0\)。用户指定样本数量\(n\)的大小。\(n\)越大，精度越高，但是计算量越大。
2. 把下面的步骤重复\(n\)次：(a). 从区间 ([-1,1]) 上做两次均匀随机抽样得到实数\(x\)和\(y\)。(b). 如果\(x^2+y^2\leq1\), 那么\(m \leftarrow m+1\)。
3. 返回\(\frac{4m}{n}\)作为对\(\pi\)的估计。

大数定律保证了蒙特卡洛的正确性：当\(n\)趋于无穷，\(\frac{4m}{n}\)趋于\(\pi\)。其实还能进一步用概率不等式分析误差的上界。比如使用 Bernstein 不等式，可以证明出下面结论：

\(\left\|\frac{4m}{n}-\pi\right\|=O\left(\frac{1}{\sqrt{n}}\right).\)

这个不等式说明\(\frac{4m}{n}\)(即对\(\pi\)的估计) 会收敛到\(\pi\), 收敛率是\(\frac{1}{\sqrt{n}}\)。然而这个收敛率并不快：样本数量\(n\)增加一万倍，精度才能提高一百倍。

例二：估算阴影部分面积

图2.4中有正方形、圆、扇形，几个形状相交。请估算阴影部分面积。这个问题常见于初中数学竞赛。假如你不会微积分，也不会几何技巧，你是否有办法近似估算阴影部分面积呢？用蒙特卡洛可以很容易解决这个问题。

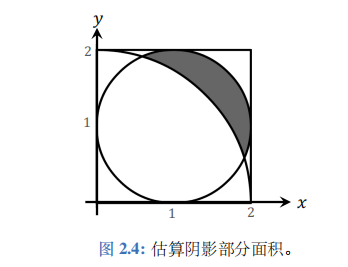
图 2.5 中绿色圆的圆心是 (1,1), 半径等于 1;蓝色扇形的圆心是 (0,0)、半径等于2。目的点\((x,y)\)在绿色的圆中，而不在蓝色的扇形中。

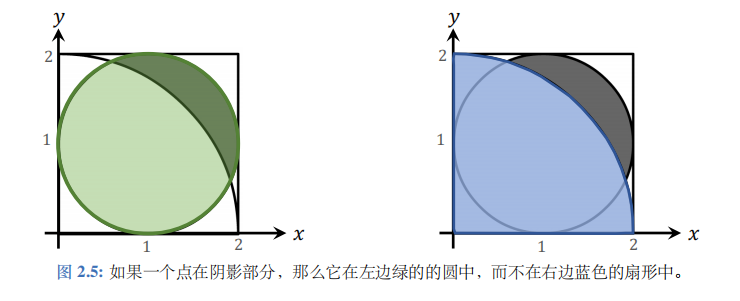
利用圆的方程可以判定点\((x,y)\)是否在绿色圆里面。如果\((x,y)\)满足方程\((x-1)^2+(y-1)^2\leq1\),

则说明\((x,y)\)在绿色圆里面。

利用扇形的方程可以判定点\((x,y)\)是否在蓝色扇形外面。如果点\((x,y)\)满足方程

\(x^2+y^2>4\),

则说明\((x,y)\)在蓝色扇形外面。

如果一个点同时满足方程 (2.1)和 (2.2),那么这个点一定在阴影区域内。从\([0,2] \times [0,2]\)这个正方形中做随机抽样，得到\(n\)个点。然后用两个方程筛选落在阴影部分的点。

我们在正方形\([0,2] \times [0,2]\)中随机均匀抽样，得到的点有一定概率会落在阴影部分。我们来计算这个概率。正方形的边长等于2，所以面积\(a_1=4\)。设阴影部分面积为\(a_2\)。那么点落在阴影部分概率是

\(p=\frac{a_2}{a_1}=\frac{a_2}{4}\)。

我们从正方形中随机抽\(n\)个点，设有\(M\)个点落在阴影部分内(\(M\)是个随机变量)。每个点落在阴影部分的概率是\(p\),所以\(M\)的期望等于\(\mathbb{E}[M]=np=\frac{na_2}{4}\)。

用方程 (2.1)和 (2.2) 对\(n\)个点做筛选，发现实际上有\(m\)个点落在阴影部分内 (\(m\)是随机变量\(M\)的观测值)。如果\(n\)很大，那么\(m\)会比较接近期望\(\mathbb{E}[M]=\frac{na_2}{4}\), 即\(m \approx \frac{na_2}{4}\)。

也即\(a_2 \approx \frac{4m}{n}\)。

这个公式就是对阴影部分面积的估计。我们依据这个公式做编程实现。下面是伪代码：

1. 初始化\(m=0\)。用户指定样本数量\(n\)的大小。\(n\)越大，精度越高，但是计算量越大。
2. 把下面的步骤重复\(n\)次：(a). 从区间\([0,2]\)上均匀随机抽样得到\(x\); 再做一次均匀随机抽样，得到\(y\)。(b). 如果\((x-1)^2+(y-1)^2\leq1\)和\(x^2+y^2>4\)两个不等式都成立，那么让\(m \leftarrow m+1\)。
3. 返回\(\frac{4m}{n}\)作为对阴影部分面积的估计。

例三：近似定积分

近似求积分是蒙特卡洛最重要的应用之一，在科学和工程中有广泛的应用。举个例子，给定一个函数：

\(f(x)=\frac{1}{1+(\sin x)\cdot(\ln x)^2},\)

要求计算\(f\)在区间 0.8 到 3 上的定积分：

\(I=\int_{0.8}^{3}f(x)dx.\)

有很多科学和工程问题需要计算定积分，而函数\(f(x)\)可能很复杂，求定积分会很困难，甚至有可能不存在解析解。如果求解析解很困难，或者解析解不存在，则可以用蒙特卡洛近似计算数值解。

一元函数的定积分 是相对比较简单的问题。一元函数的意思是变量\(x\)是个标量。给定一元函数\(f(x)\), 求函数在\(a\)到\(b\)区间上的定积分：

\(I=\int_{a}^{b}f(x)dx.\)

蒙特卡洛方法通过下面的步骤近似定积分：

1. 在区间\([a,b]\)上做随机抽样，得到\(n\)个样本，记作：\(x_1,\cdots,x_n\)。样本数量\(n\)由用户自己定，\(n\)越大，计算量越大，近似越准确。
2. 对函数值\(f(x_1),\cdots,f(x_n)\)求平均，再乘以区间长度\(b-a\):

\(q_n=(b-a)\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_i).\)

3. 返回\(q_n\)作为定积分\(I\)的估计值。

多元函数的定积分 要复杂一些。设\(f:\mathbb{R}^d\mapsto\mathbb{R}\)是一个多元函数，变量\(x\)是\(d\)维向量。要求计算\(f\)在集合\(\Omega\)上的定积分：

\(I=\int_{\Omega}f(\boldsymbol{x})d\boldsymbol{x}.\)

蒙特卡洛方法通过下面的步骤近似定积分：

1. 在集合\(\Omega\)上做均匀随机抽样，得到\(n\)个样本，记作向量\(x_1,\cdots,x_n\)。样本数量\(n\)由用户自己定，\(n\)越大，计算量越大，近似越准确。
2. 计算集合\(\Omega\)的体积：\(v=\int_{\Omega}d\boldsymbol{x}.\)
3. 对函数值\(f(x_1),\cdots,f(x_n)\)求平均，再乘以\(\Omega\)的体积\(v\):

\(q_n=v\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_i).\)(2.3)

4. 返回\(q_n\)作为定积分\(I\)的估计值。

注意，算法第二步需要求\(\Omega\)的体积。如果\(\Omega\)是长方体、球体等规则形状，那么可以解析地算出体积\(v\)。可是如果\(\Omega\)是不规则形状，那么就需要定积分求\(\Omega\)的体积\(v\), 这是比较困难的。可以用类似于上一小节“求阴影部分面积”的方法近似计算体积\(v\)。

举例讲解多元函数的蒙特卡洛积分：这个例子中被积分的函数是二元函数：

\(f(x,y)=\left\{\begin{array}{ll}1,&\text{if }x^2+y^2\leq1;\\0,&\text{otherwise}.\end{array}\right.\)(2.4)

直观地说，如果点\((x,y)\)落在右图的绿色圆内，那么函数值就是 1; 否则函数值就是 0。定义集合\(\Omega=[-1,1]\times[-1,1]\), 即右图中蓝色的正方形，它的面积是\(v=4\)。

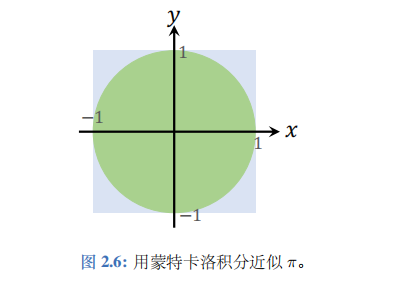
定积分\(I=\int_{\Omega}f(x,y)dxdy\)

等于多少呢？很显然，定积分等于圆的面积，即\(\pi \cdot 1^2=\pi\)。因此，定积分\(I=\pi\)。用蒙特卡洛求出\(I\),就得到了\(\pi\)。从集合\(\Omega=[-1,1]\times[-1,1]\)上均匀随机抽样\(n\)个点，记作\((x_1,y_1),\cdots,(x_n,y_n)\)。应用公式(2.3), 可得

\(q_n=v\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_i,y_i)=\frac{4}{n}\sum_{i=1}^{n}f(x_i,y_i).\)(2.5)

把\(q_n\)作为对定积分\(I=\pi\)的近似。这与前面近似\(\pi\)的算法完全相同，区别在于此处的算法是从另一个角度推导出的。

例四：近似期望

蒙特卡洛还可以用来近似期望，这在整本书中会反复应用。设\(X\)是\(d\)维随机变量，它的取值范围是集合\(\Omega \subset \mathbb{R}^d\)。函数\(p(x)\)是\(X\)的概率密度函数。设\(f:\Omega \mapsto \mathbb{R}\)是任意的多元函数，它关于变量\(X\)的期望是：

\(\mathbb{E}_{X\sim p(\cdot)}\Big[f(X)\Big]=\int_{\Omega}p(x)\cdot f(x)d x.\)

由于期望是定积分，所以可以按照上一小节的方法，用蒙特卡洛求定积分。上一小节在集合\(\Omega\)上做均匀抽样，用得到的样本近似上面公式中的定积分。

下面介绍一种更好的算法。既然我们知道概率密度函数\(p(x)\), 我们最好是按照\(p(x)\)做非均匀抽样，而不是均匀抽样。按照\(p(x)\)做非均匀抽样，可以比均匀抽样有更快的收敛。具体步骤如下：

1. 按照概率密度函数\(p(x)\),在集合\(\Omega\)上做非均匀随机抽样，得到\(n\)个样本，记作向量\(x_1,\cdots,x_n \sim p(\cdot)\)。样本数量\(n\)由用户自己定，\(n\)越大，计算量越大；近似越准确。
2. 对函数值\(f(x_1),\cdots,f(x_n)\)求平均：

\(q_n=\frac{1}{n}\sum_{i=1}^{n}f(x_i).\)

3. 返回\(q_n\)作为期望\(\mathbb{E}_{X\sim p(\cdot)}\Big[f(X)\Big]\)的估计值。

注 如果按照上述方式做编程实现，需要储存函数值\(f(x_1),\cdots,f(x_n)\)。但用如下的方式做编程实现，可以减小内存开销。初始化\(q_0=0\)。从\(t=1\)到\(n\),依次计算

\(q_t=(1-\frac{1}{t})\cdot q_{t-1}+\frac{1}{t}\cdot f(x_t).\)(2.6)

不难证明，这样得到的\(q_n\)等于\(\frac{1}{n}\sum_{i=1}^{n}f(x_i)\)。这样无需存储所有的\(f(x_1),\cdots,f(x_n)\)。可以进一步把公式(2.6) 中的\(\frac{1}{t}\)替换成\(\alpha_t\),得到公式：

\(q_t=(1-\alpha_t)\cdot q_{t-1}+\alpha_t\cdot f(x_t).\)

这个公式叫做 Robbins-Monro 算法，其中\(\alpha_n\)称为学习步长或学习率。只要\(\alpha_t\)满足下面的性质，就能保证算法的正确性：

\(\lim_{n\to\infty}\sum_{t=1}^{n}\alpha_t=\infty\)和\(\lim_{n\to\infty}\sum_{t=1}^{n}\alpha_t^2<\infty.\)

显然，\(\alpha_t=\frac{1}{t}\)满足上述性质。Robbins-Monro 算法可以应用在 Q 学习算法中。

例五：随机梯度

我们可以用蒙特卡洛近似期望来理解随机梯度算法。

设随机变量\(X\)为一个数据样本，令\(w\)为神经网络的参数。设\(p(x)\)为随机变量\(X\)的概率密度函数。定义损失函数\(L(X;w)\)。它的值越小，意味着模型做出的预测越准确；反之，它的值越大，则意味着模型做出的预测越差。因此，我们希望调整神经网络的参数\(w\), 使得损失函数的期望尽量小。神经网络的训练可以定义为这样的优化问题：

\(\min_{\boldsymbol{w}}\mathbb{E}_{X\sim p(\cdot)}\Big[L(X;\boldsymbol{w})\Big].\)

目标函数\(\mathbb{E}_X[L(X;\boldsymbol{w})]\)关于\(\boldsymbol{w}\)的梯度是：

\(\boldsymbol{g} \triangleq \nabla_{\boldsymbol{w}}\mathbb{E}_{X\sim p(\cdot)}\Big[L(X;\boldsymbol{w})\Big]=\mathbb{E}_{X\sim p(\cdot)}\Big[\nabla_{\boldsymbol{w}}L(X;\boldsymbol{w})\Big].\)(2.7)

可以做梯度下降更新\(\boldsymbol{w}\), 以减小目标函数\(\mathbb{E}_X[L(X;\boldsymbol{w})]\):

\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \boldsymbol{g}.\)

此处的\(\alpha\)被称作学习率 (learning rate)。直接计算梯度\(\boldsymbol{g}\)通常会比较慢。为了加速计算，可以对期望

\(\boldsymbol{g}=\mathbb{E}_{X\sim p(\cdot)}\Big[\nabla_{\boldsymbol{w}}L(X;\boldsymbol{w})\Big]\)

做蒙特卡洛近似，把得到的近似梯度\(\tilde{\boldsymbol{g}}\)称作随机梯度 (stochastic gradient), 用\(\tilde{\boldsymbol{g}}\)代替\(\boldsymbol{g}\)来更新\(\boldsymbol{w}\)。

1. 根据概率密度函数\(p(x)\)做随机抽样，得到\(B\)个样本，记作\(\tilde{x}_1,\ldots,\tilde{x}_B\)。
2. 计算梯度\(\nabla_{\boldsymbol{w}}L(\tilde{x}_j;\boldsymbol{w}), \forall j=1,\ldots,B\)。对它们求平均：

\(\tilde{\boldsymbol{g}}:=\frac{1}{B}\sum_{j=1}^{B}\nabla_{\boldsymbol{w}}L(\tilde{x}_j;\boldsymbol{w}).\)

我们称\(\tilde{\boldsymbol{g}}\)为 随机梯度。因为\(\mathbb{E}[\tilde{\boldsymbol{g}}]=\boldsymbol{g}\), 它是\(\boldsymbol{g}\)的一个无偏估计。

3. 做随机梯度下降更新\(\boldsymbol{w}\):

\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \tilde{\boldsymbol{g}}.\)

样本数量\(B\)称作批量大小 (batch size), 通常是一个比较小的正整数，比如 1、8、16、32。所以我们称之为 最小批 (mini-batch) SGD。

在实际应用中，样本真实的概率密度函数\(p(x)\)一般是未知的。在训练神经网络的时候，我们通常会收集一个训练数据集\(\mathcal{X}=\{x_1,\cdots,x_n\}\), 并求解这样一个经验风险最小化 (empirical risk minimization) 问题：

\(\min_{\boldsymbol{w}}\frac{1}{n}\sum_{i=1}^{n}L(\boldsymbol{x}_i;\boldsymbol{w}).\)(2.8)

这相当于我们用下面这个概率质量函数代替真实的\(p(x)\):

\(p(x) = \begin{cases} \frac{1}{n}, & \text{如果 } x \in \mathcal{X}; \\ 0, & \text{如果 } x \notin \mathcal{X}. \end{cases}\)

公式的意思是随机变量\(X\)的取值是\(n\)个数据点中的一个，概率都是\(\frac{1}{n}\)。那么最小批 SGD 的每一轮都从集合\(\{x_1,\cdots,x_n\}\)中均匀随机抽取\(B\)个样本，计算随机梯度，更新模型参数\(\boldsymbol{w}\)。

总结

本文详细讲解了蒙特卡洛的应用。其中最重要的知识点是蒙特卡洛近似期望：设\(X\)是随机变量，\(x\)是观测值，蒙特卡洛用\(f(x)\)近似期望\(\mathbb{E}[f(X)]\)。强化学习中的 Q 学习、SARSA、策略梯度等算法都需要这样用蒙特卡洛近似期望。