4.1 Sarsa算法
TD 算法是一大类算法的总称。Q 学习是一种 TD 算法,Q 学习的目的是学习最优动作价值函数\(Q^*\)。这里介绍 SARSA, 它也是一种 TD 算法,SARSA 的目的是学习动作价值函数\(Q_\pi(s, a)\)。
表格形式的 SARSA
假设状态空间\(S\)和动作空间\(\mathcal{A}\)都是有限集,即集合中元素数量有限。比如,\(S\)中一共有 3 种状态,\(\mathcal{A}\)中一共有 4 种动作。那么动作价值函数\(Q_\pi(s, a)\)可以表示为一个 3×4 的表格,比如右边的表格。该表格与一个策略函数\(\pi(a|s)\)相关联;如果\(\pi\)发生变化, 表格\(Q_\pi\)也会发生变化。
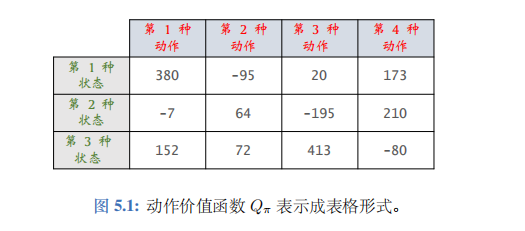
我们用表格\(q\)近似\(Q_\pi\)。该如何通过智能体与环境的交互来学习表格\(q\)呢?首先初始化\(q\),可以让它是全零的表格。然后用表格形式的 SARSA 算法更新\(q\), 每次更新表格的一个元素。最终\(q\)收敛到\(Q_\pi\)。
推导 :
SARSA 算法由下面的贝尔曼方程推导出:
\(Q_\pi(s_t, a_t) = \mathbb{E}_{S_{t+1}, A_{t+1}} \big[R_t + \gamma \cdot Q_\pi(S_{t+1}, A_{t+1}) \big| S_t = s_t, A_t = a_t\big]\)
我们对贝尔曼方程左右两边做近似:
- 方程左边的\(Q_\pi(s_t, a_t)\)可以近似成\(q(s_t, a_t)\)。
- 方程右边的期望是关于下一时刻状态\(S_{t+1}\)和动作\(A_{t+1}\)求的。给定当前状态\(s_t\), 智能体执行动作\(a_t\),环境会给出奖励\(r_t\)和新的状态\(s_{t+1}\)。然后基于\(s_{t+1}\)做随机抽样,得到新的动作\(\tilde{a}_{t+1} \sim \pi(\cdot|s_{t+1})\)。用观测到的\(r_t\)、\(s_{t+1}\)和计算出的\(\tilde{a}_{t+1}\)对期望做蒙特卡洛近似,得到:
\(r_t + \gamma \cdot Q_\pi(s_{t+1}, \tilde{a}_{t+1})\).
- 进一步把公式中的\(Q_\pi\)近似成\(q\), 得到
\(\hat{y}_t \triangleq r_t + \gamma \cdot q(s_{t+1}, \tilde{a}_{t+1})\).
把它称作 TD 目标。它是表格在\(t+1\)时刻对\(Q_\pi(s_t, a_t)\)做出的估计。
\(q(s_t, a_t)\)和\(\hat{y}_t\)都是对动作价值\(Q_\pi(s_t, a_t)\)的估计。
由于\(\hat{y}_t\)部分基于真实观测到的奖励\(r_t\), 我们认为\(\hat{y}_t\)是更可靠的估计,所以鼓励\(q(s_t, a_t)\)趋近\(\hat{y}_t\)。更新表格\((s_t, a_t)\)位置上的元素:
\(q(s_t, a_t) \leftarrow (1-\alpha) \cdot q(s_t, a_t) + \alpha \cdot \hat{y}_t.\)
这样可以使得\(q(s_t, a_t)\)更接近\(\hat{y}_t\)。
SARSA 是 State-Action-Reward-State-Action 的缩写,原因是 SARSA 算法用到了这个五元组\((s_t, a_t, r_t, s_{t+1}, \tilde{a}_{t+1})\)。SARSA 算法学到的\(q\)依赖于策略\(\pi\), 这是因为五元组中的\(\tilde{a}_{t+1}\)是根据\(\pi(\cdot|s_{t+1})\)抽样得到的。
训练流程:
设当前表格为\(q_{\text{now}}\), 当前策略为\(\pi_{\text{now}}\)。每一轮更新表格中的一个元素, 把更新之后的表格记作\(q_{\text{new}}\)。
- 观测到当前状态\(s_t\),根据当前策略做抽样\(a_t \sim \pi_{\text{now}}(\cdot|s_t)\)。
- 把表格\(q_{\text{now}}\)中第\((s_t, a_t)\)位置上的元素记作:\(\hat{q}_t = q_{\text{now}}(s_t, a_t)\).
- 智能体执行动作\(a_t\)之后,观测到奖励\(r_t\)和新的状态\(s_{t+1}\)。
- 根据当前策略做抽样\(\tilde{a}_{t+1} \sim \pi_{\text{now}}(\cdot|s_{t+1})\)。注意,\(\tilde{a}_{t+1}\)只是假想的动作,智能体不予执行。
- 把表格\(q_{\text{now}}\)中第\((s_{t+1}, \tilde{a}_{t+1})\)位置上的元素记作:\(\hat{q}_{t+1} = q_{\text{now}}(s_{t+1}, \tilde{a}_{t+1})\).
- 计算 TD 目标和 TD 误差:\(\hat{y}_t = r_t + \gamma \cdot \hat{q}_{t+1}, \quad \delta_t = \hat{q}_t - \hat{y}_t\).
- 更新表格中\((s_t, a_t)\)位置上的元素:\(q_{\text{new}}(s_t, a_t) \leftarrow q_{\text{now}}(s_t, a_t) - \alpha \cdot \delta_t\).
- 用某种算法更新策略函数。该算法与 SARSA 算法无关。
神经网络形式的 SARSA
价值网络:
如果状态空间\(S\)是无限集,那么我们无法用一张表格表示\(Q_\pi\), 否则表格的行数是无穷。一种可行的方案是用一个神经网络\(q(s, a; \boldsymbol{w})\)来近似\(Q_\pi(s, a)\); 理想情况下,\(q(s, a; \boldsymbol{w}) = Q_\pi(s, a), \forall s \in \mathcal{S}, a \in \mathcal{A}\).
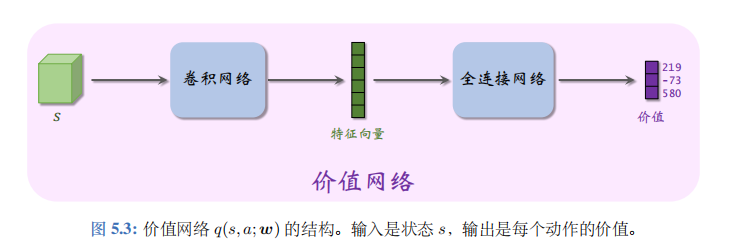
神经网络\(q(s, a; \boldsymbol{w})\)被称为价值网络 (value network), 其中的\(\boldsymbol{w}\)表示神经网络中可训练的参数。神经网络的结构是人预先设定的 (比如有多少层,每一层的宽度是多少),而参数\(\boldsymbol{w}\)需要通过智能体与环境的交互来学习。首先随机初始化\(\boldsymbol{w}\),然后用 SARSA 算法更新\(\boldsymbol{w}\)。
神经网络的结构见图 5.3。价值网络的输入是状态\(s\)。如果\(s\)是矩阵或张量 (tensor), 那么可以用卷积网络处理\(s\)(如图 5.3)。如果\(s\)是向量,那么可以用全连接层处理\(s\)。价值网络的输出是每个动作的价值。动作空间\(\mathcal{A}\)中有多少种动作,则价值网络的输出就是多少维的向量,向量每个元素对应一个动作。举个例子,动作空间是\(\{左,右,上\}\), 价值网络的输出是
\(q(s, 左; \boldsymbol{w}) = 219, q(s, 右; \boldsymbol{w}) = -73, q(s, 上; \boldsymbol{w}) = 580\).
算法推导:
给定当前状态\(s_t\), 智能体执行动作\(a_t\), 环境会给出奖励\(r_t\)和新的状态\(s_{t+1}\)。然后基于\(s_{t+1}\)做随机抽样,得到新的动作\(\tilde{a}_{t+1} \sim \pi(\cdot|s_{t+1})\)。定义 TD 目标:
\(\hat{y}_t \triangleq r_t + \gamma \cdot q(s_{t+1}, \tilde{a}_{t+1}; \boldsymbol{w}).\)
我们鼓励\(q(s_t, a_t; \boldsymbol{w})\)接近 TD 目标\(\hat{y}_t\), 所以定义损失函数:
\(L(\boldsymbol{w}) \triangleq \frac{1}{2} \Big[q(s_t, a_t; \boldsymbol{w}) - \hat{y}_t\Big]^2.\)
损失函数的变量是\(\boldsymbol{w}\), 而\(\hat{y}_t\)被视为常数。(尽管\(\hat{y}_t\)也依赖于参数\(\boldsymbol{w}\), 但这一点被忽略掉.) 设\(\hat{q}_t = q(s_t, a_t; \boldsymbol{w})\)。损失函数关于\(\boldsymbol{w}\)的梯度是:
\(\nabla_{\boldsymbol{w}} L(\boldsymbol{w}) = (\hat{q}_t - \hat{y}_t) \cdot \nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}).\)
做一次梯度下降更新\(\boldsymbol{w}\):
\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}).\)
这样可以使得\(q(s_t, a_t; \boldsymbol{w})\)更接近\(\hat{y}_t\)。此处的\(\alpha\)是学习率,需要手动调整。
训练流程:
设当前价值网络的参数为\(\boldsymbol{w}_{\text{now}}\), 当前策略为\(\pi_{\text{now}}\)。每一轮训练用五元组\((s_t, a_t, r_t, s_{t+1}, \tilde{a}_{t+1})\)对价值网络参数做一次更新。
- 观测到当前状态\(s_t\),根据当前策略做抽样:\(a_t \sim \pi_{\text{now}}(\cdot|s_t)\)。
- 用价值网络计算\((s_t, a_t)\)的价值:\(\hat{q}_t = q(s_t, a_t; \boldsymbol{w}_{\text{now}})\).
- 智能体执行动作\(a_t\)之后,观测到奖励\(r_t\)和新的状态\(s_{t+1}\)。
- 根据当前策略做抽样\(\tilde{a}_{t+1} \sim \pi_{\text{now}}(\cdot|s_{t+1})\)。注意,\(\tilde{a}_{t+1}\)只是假想的动作,智能体不予执行。
- 用价值网络计算\((s_{t+1}, \tilde{a}_{t+1})\)的价值:\(\hat{q}_{t+1} = q(s_{t+1}, \tilde{a}_{t+1}; \boldsymbol{w}_{\text{now}})\).
- 计算 TD 目标和 TD 误差:\(\hat{y}_t = r_t + \gamma \cdot \hat{q}_{t+1}, \quad \delta_t = \hat{q}_t - \hat{y}_t\).
- 对价值网络\(q\)做反向传播,计算\(q\)关于\(\boldsymbol{w}\)的梯度:\(\nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}_{\text{now}})\).
- 更新价值网络参数:\(\boldsymbol{w}_{\text{new}} \leftarrow \boldsymbol{w}_{\text{now}} - \alpha \cdot \delta_t \cdot \nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}_{\text{now}})\).
- 用某种算法更新策略函数。该算法与 SARSA 算法无关。