4.2 Q-learning算法
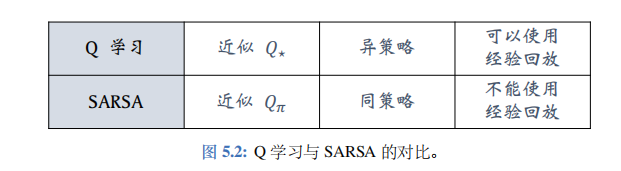
Q 学习与 SARSA 的对比:
Q学习不依赖于\(\pi\), 因此Q学习属于异策略 (off-policy), 可以用经验回放。而 SARSA 依赖于\(\pi\), 因此 SARSA 属于同策略(on-policy), 不能用经验回放。两种算法的对比如图 5.2 所示。
Q学习的目标是学到表格\(\tilde{Q}\), 作为最优动作价值函数\(Q^*\)的近似。因为\(Q^*\)与\(\pi\)无关,所以在理想情况下,不论收集经验用的行为策略\(\pi\)是什么,都不影响 Q学习得到的最优动作价值函数。因此,Q学习属于异策略(off-policy),允许行为策略区别于目标策略。Q学习允许使用经验回放,可以重复利用过时的经验。
SARSA 算法的目标是学到表格\(q\),作为动作价值函数\(Q_\pi\)的近似。\(Q_\pi\)与一个策略\(\pi\)相对应,用不同的策略\(\pi\), 对应\(Q_\pi\)就会不同。策略\(\pi\)越好,\(Q_\pi\)的值越大。经验回放数组里的经验\((s_j, a_j, r_j, s_{j+1})\)是过时的行为策略\(\pi_{\text{old}}\)收集到的,与当前策略\(\pi_{\text{now}}\)应的价值\(Q_{\pi_{\text{now}}}\)对应不上。想要学习\(Q_\pi\)的话,必须要用与当前策略\(\pi_{\text{now}}\)收集到的经验,而不能用过时的\(\pi_{\text{old}}\)收集到的经验。这就是为什么 SARSA 不能用经验回放的原因。
Q学习算法
Q学习算法上一节用 TD 算法训练 DQN(介绍DQN的笔记在这里:深度强化学习(王树森)笔记02), 更准确地说,我们用的 TD 算法叫做 Q 学习算法 (Q- learning)。TD 算法是一大类算法,常见的有 Q 学习和 SARSA。Q 学习的目的是学到最优动作价值函数\(Q^*\),而 SARSA 的目的是学习动作价值函数\(Q_\pi\)。下一章会介绍 SARSA 算法。
Q 学习是在 1989 年提出的,而 DQN 则是 2013 年才提出。从 DQN 的名字 (深度 Q 网络)就能看出 DQN 与 Q 学习的联系。最初的 Q 学习都是以表格形式出现的。虽然表格形式的 Q 学习在实践中不常用,但还是建议读者有所了解。
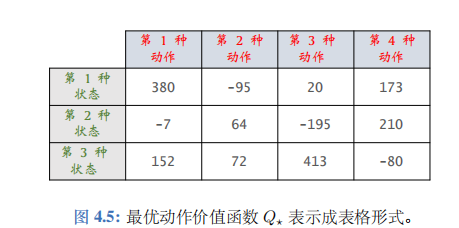
用表格表示\(Q^*\):
假设状态空间\(S\)和动作空间\(\mathcal{A}\)都是有限集,即集合中元素数量有限。比如,\(S\)中一共有3种状态,\(\mathcal{A}\)中一共有4种动作。那么最优动作价值函数\(Q^*(s,a)\)可以表示为一个3×4的表格,比如右边的表格。基于当前状态\(s_t\),做决策时使用的公式\(a_t = \mathop{\mathrm{argmax}}_{a \in \mathcal{A}} Q^*(s_t,a)\)的意思是找到\(s_t\)对应的行(3行中的某一行),找到该行最大的价值,返回该元素对应的动作。举个例子,当前状态\(s_t\)是第2种状态,那么我们查看第2行,发现该行最大的价值是210, 对应第4种动作。那么应当执行的动作\(a_t\)就是第4种动作。
该如何通过智能体的轨迹来学习这样一个表格呢?答案是用一个表格\(\tilde{Q}\)来近似\(Q^*\)。
首先初始化\(\tilde{Q}\),可以让它是全零的表格。然后用表格形式的 Q学习算法更新\(\tilde{Q}\), 每次更新表格的一个元素。最终\(\tilde{Q}\)会收敛到\(Q^*\)。
算法推导:
首先复习一下最优贝尔曼方程:
\(Q^*(s_t, a_t) = \mathbb{E}_{S_{t+1} \sim p(\cdot|s_t, a_t)} \Big[ R_t + \gamma \cdot \max_{A \in \mathcal{A}} Q^*(S_{t+1}, A) \Big| S_t = s_t, A_t = a_t \Big].\)
我们对方程左右两边做近似:
- 方程左边的\(Q^*(s_t, a_t)\)可以近似成\(\tilde{Q}(s_t, a_t)\)。
- 方程右边的期望是关于下一时刻状态\(S_{t+1}\)求的。给定当前状态\(s_t\), 智能体执行动作\(a_t\),环境会给出奖励\(r_t\)和新的状态\(s_{t+1}\)。用观测到的\(r_t\)和\(s_{t+1}\)对期望做蒙特卡洛近似,得到:\(r_t + \gamma \cdot \max_{a \in \mathcal{A}} Q^*(s_{t+1}, a)\).
- 进一步把公式中的\(Q^*\)近似成\(\tilde{Q}\), 得到
\(\widehat{y}_{t} \triangleq r_{t} + \gamma \cdot \max_{a \in \mathcal{A}} \widetilde{Q}(s_{t+1}, a).\)
把它称作 TD 目标。它是表格在 t+1时刻对\(Q^*(s_t, a_t)\)做出的估计。
\(\tilde{Q}(s_t, a_t)\)和\(\hat{y}_t\)都是对最优动作价值\(Q^*(s_t, a_t)\)的估计。由于\(\hat{y}_t\)部分基于真实观测到的奖励\(r_t\),我们认为\(\hat{y}_t\)是更可靠的估计,所以鼓励\(\tilde{Q}(s_t, a_t)\)更接近\(\hat{y}_t\)。更新表格\(\tilde{Q}\)中\((s_t, a_t)\)位置上的元素:
\(\tilde{Q}(s_t, a_t) \leftarrow (1-\alpha) \cdot \tilde{Q}(s_t, a_t) + \alpha \cdot \hat{y}_t.\)
这样可以使得\(\tilde{Q}(s_t, a_t)\)更接近\(\hat{y}_t\)。Q 学习的目的是让\(\tilde{Q}\)逐渐趋近于\(Q^*\)。
收集训练数据:
Q学习更新\(\tilde{Q}\)的公式不依赖于具体的策略。我们可以用任意策略控制智能体,与环境交互,把得到的轨迹划分成\((s_t, a_t, r_t, s_{t+1})\)这样的四元组,存入经验回放数组。这个控制智能体的策略叫做行为策略(behavior policy), 比较常用的行为策略是\(\epsilon\)-greedy:
\(a_t = \left\{ \begin{array}{ll} \mathrm{argmax}_a \tilde{Q}(s_t, a), & \text{以概率 } (1-\epsilon); \\ \text{均匀抽取 } A \text{ 中的一个动作}, & \text{以概率 } \epsilon. \end{array} \right.\)
事后用经验回放更新表格\(\tilde{Q}\), 可以重复利用收集到的四元组。
经验回放更新表格\(\tilde{Q}\):
随机从经验回放数组中抽取一个四元组,记作\((s_j, a_j, r_j, s_{j+1})\)。设当前表格为\(\tilde{Q}_{\text{now}}\)。更新表格中\((s_j, a_j)\)位置上的元素,把更新之后的表格记作\(\tilde{Q}_{\text{new}}\)。
- 把表格\(\tilde{Q}_{\text{now}}\)中第\((s_j, a_j)\)位置上的元素记作:\(\hat{q}_j = \tilde{Q}_{\text{now}}(s_j, a_j)\).
- 查看表格\(\tilde{Q}_{\text{now}}\)的第\(s_{j+1}\)行,把该行的最大值记作:\(\hat{q}_{j+1} = \max_a \tilde{Q}_{\text{now}}(s_{j+1}, a)\).
- 计算 TD 目标和 TD 误差:\(\hat{y}_j = r_j + \gamma \cdot \hat{q}_{j+1}, \quad \delta_j = \hat{q}_j - \hat{y}_j\).
- 更新表格中\((s_j, a_j)\)位置上的元素:\(\tilde{Q}_{\text{new}}(s_j, a_j) \leftarrow \tilde{Q}_{\text{now}}(s_j, a_j) - \alpha \cdot \delta_j\).
收集经验与更新表格\(\tilde{Q}\)可以同时进行。每当智能体执行一次动作,我们可以用经验回放对\(\tilde{Q}\)做几次更新。也可以每当完成一局游戏,对\(\tilde{Q}\)做几次更新。
同策略 (On-policy) 与异策略 (Off-policy)
在强化学习中经常会遇到两个专业术语:同策略(on-policy) 和异策略 (off-policy)。
为了解释同策略和异策略,我们要从行为策略 (behavior policy) 和目标策略 (target policy) 讲起。
在强化学习中,我们让智能体与环境交互,记录下观测到的状态、动作、奖励,用这些经验来学习一个策略函数。在这一过程中,控制智能体与环境交互的策略被称作行为策略。行为策略的作用是收集经验(experience),即观测的状态、动作、奖励。
强化学习的目的是得到一个策略函数,用这个策略函数来控制智能体。这个策略函数就叫做目标策略。在本章中,目标策略是一个确定性的策略,即用 DQN 控制智能体:
\(a_t := \underset{a}{\operatorname*{argmax}}\: Q(s_t, a; \boldsymbol{w}).\)
本章的 Q 学习算法用任意的行为策略收集\((s_t, a_t, r_t, s_{t+1})\)这样的四元组,然后拿它们训练目标策略,即 DQN。
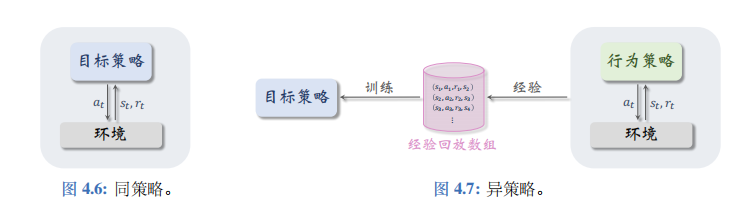
行为策略和目标策略可以相同,也可以不同。同策略是指用相同的行为策略和目标策略,后面章节会介绍同策略。异策略是指用不同的行为策略和目标策略,本章的 DQN 属于异策略。同策略和异策略如图 4.6、4.7 所示。
由于DQN 是异策略,行为策略可以不同于目标策略,可以用任意的行为策略收集经验,比如最常用的行为策略是 \(\epsilon-greedy\):
\(a_{t} = \left\{ \begin{array}{ll} \operatorname{argmax}_{a} Q(s_{t}, a; w), & \text{以概率}(1-\epsilon); \\ \text{均匀抽取}\mathcal{A}\text{中的一个动作}, & \text{以概率}\epsilon. \end{array} \right.\)
让行为策略带有随机性的好处在于能探索更多没见过的状态。在实验中,初始的时候让\(\epsilon\)比较大 (比如\(\epsilon=0.5)\); 在训练的过程中,让\(\epsilon\)逐渐衰减,在几十万步之后衰减到较小的值(\(\epsilon=0.01\)), 此后固定住\(\epsilon=0.01\)。
异策略的好处是可以用行为策略收集经验,把\((s_t, a_t, r_t, s_{t+1})\)这样的四元组记录到一个数组里,在事后反复利用这些经验去更新目标策略。这个数组被称作经验回放数组(replay buffer), 这种训练方式被称作经验回放 (experience replay)。注意,经验回放只适用于异策略,不适用于同策略,其原因是收集经验时用的行为策略不同于想要训练出的目标策略。
总结
DQN 是对最优动作价值函数\(Q^*\)的近似。DQN 的输入是当前状态\(s_t\), 输出是每个动作的 Q 值。DQN 要求动作空间\(\mathcal{A}\)是离散集合,集合中的元素数量有限。如果动作空间\(\mathcal{A}\)的大小是 k,那么 DQN 的输出就是 k 维向量。DQN 可以用于做决策,智能体执行 Q 值最大的动作。
TD 算法的目的在于让预测更接近实际观测。以驾车问题为例,如果使用 TD 算法,无需完成整个旅途就能做梯度下降更新模型。请读者理解并记忆 TD 目标、TD 误差的定义,它们将出现在所有价值学习的章节中。
Q 学习算法是 TD 算法的一种,可以用于训练 DQN。Q 学习算法由最优贝尔曼方程推导出。Q 学习算法属于异策略,允许使用经验回放。由任意行为策略收集经验, 存入经验回放数组。事后做经验回放,用 TD 算法更新 DQN 参数。
如果状态空间\(S\)、动作空间\(\mathcal{A}\)都是较小的有限离散集合,那么可以用表格形式的Q学习算法学习\(Q^*\)。如今表格形式的 Q 学习已经不常用。