4.3 多步 TD目标
多步 TD 目标
首先回顾一下 SARSA 算法。给定五元组\((s_t, a_t, r_t, s_{t+1}, a_{t+1})\), SARSA 计算 TD 目标:
\(\hat{y}_t = r_t + \gamma \cdot q(s_{t+1}, a_{t+1}; \boldsymbol{w}).\)
公式中只用到一个奖励\(r_t\),这样得到的\(\hat{y}_t\)叫做单步 TD 目标。多步 TD 目标用\(m\)个奖励可以视作单步 TD 目标的推广。下面我们推导多步 TD 目标。
数学推导:
设一局游戏的长度为\(n\)。根据定义,\(t\)时刻的回报\(U_t\)是\(t\)时刻之后的所有奖励的加权和:
\(U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots + \gamma^{n-t} R_n.\)
同理,\(t+m\)时刻的回报可以写成:
\(U_{t+m} = R_{t+m} + \gamma R_{t+m+1} + \gamma^2 R_{t+m+2} + \cdots + \gamma^{n-t-m} R_n.\)
下面我们推导两个回报的关系。把\(U_t\)写成:
\(\begin{align*} U_{t} &= \left(R_{t} + \gamma R_{t+1} + \cdots + \gamma^{m-1} R_{t+m-1}\right) + \left(\gamma^{m} R_{t+m} + \cdots + \gamma^{n-t} R_{n}\right) \\ &= \left(\sum_{i=0}^{m-1} \gamma^{i} R_{t+i}\right) + \gamma^{m} \underbrace{\left(R_{t+m} + \gamma R_{t+m+1} + \cdots + \gamma^{n-t-m} R_{n}\right)}_{\text{等于} U_{t+m}}. \end{align*}\)
因此,回报可以写成这种形式:
\(U_t = ( \sum_{i=0}^{m-1} \gamma^i R_{t+i} ) + \gamma^m U_{t+m}.\)
动作价值函数\(Q_\pi(s_t, a_t)\)是回报\(U_t\)的期望,而\(Q_\pi(s_{t+m}, a_{t+m})\)是回报\(U_{t+m}\)的期望。利用公式,再按照贝尔曼方程的证明,不难得出下面的定理:

设\(R_k\)是\(S_k, A_k\)的函数,\(\forall k = 1, \cdots, n\)。那么
\(\underbrace{Q_\pi(s_t, a_t)}_{U_t \text{的期望}} = \mathbb{E} \left[ \left( \sum_{i=0}^{m-1} \gamma^i R_{t+i} \right) + \gamma^m \cdot \underbrace{Q_\pi(S_{t+m}, A_{t+m})}_{U_{t+m} \text{的期望}} \bigg \| S_t = s_t, A_t = a_t \right].\)
公式中的期望是关于随机变量\(S_{t+1}, A_{t+1}, \cdots, S_{t+m}, A_{t+m}\)求的。
注 回报\(U_t\)的随机性来自于\(t\)到\(n\)时刻的状态和动作:
\(S_t, A_t, S_{t+1}, A_{t+1}, \cdots, S_{t+m}, A_{t+m}, S_{t+m+1}, A_{t+m+1}, \cdots, S_n, A_n.\)
定理中把\(S_t = s_t\)和\(A_t = a_t\)看做是观测值,用期望消掉\(S_{t+1}, A_{t+1}, \cdots, S_{t+m}, A_{t+m}\), 而\(Q_\pi(S_{t+m}, A_{t+m})\)则消掉了剩余的随机变量\(S_{t+m+1}, A_{t+m+1}, \cdots, S_n, A_n\)。
多步 TD目标:
我们对定理中的期望做蒙特卡洛近似,然后再用价值网络\(q(s, a; \boldsymbol{w})\)近似动作价值函数\(Q_\pi(s, a)\)。具体做法如下:
- 在\(t\)时刻,价值网络做出预测\(\hat{q}_t = q(s_t, a_t; \boldsymbol{w})\), 它是对\(Q_\pi(s_t, a_t)\)的估计。
- 已知当前状态\(s_t\), 用策略\(\pi\)控制智能体与环境交互\(m\)次,得到轨迹\(r_t, s_{t+1}, a_{t+1}, r_{t+1}, \cdots, s_{t+m-1}, a_{t+m-1}, r_{t+m-1}, s_{t+m}, a_{t+m}\).
- 在\(t+m\)时刻,用观测到的轨迹对定理中的期望做蒙特卡洛近似,把近似的结果记作:
\(\left(\sum_{i=0}^{m-1} \gamma^i r_{t+i}\right) + \gamma^m \cdot Q_\pi(s_{t+m}, a_{t+m}).\)
- 进一步用\(q(s_{t+m}, a_{t+m}; \boldsymbol{w})\)近似\(Q_\pi(s_{t+m}, a_{t+m})\), 得到:
\(\hat{y}_t \triangleq \left(\sum_{i=0}^{m-1} \gamma^i r_{t+i}\right) + \gamma^m \cdot q(s_{t+m}, a_{t+m}; \boldsymbol{w}).\)
把\(\hat{y}_t\)称作\(m\)步TD 目标。
\(\hat{q}_t = q(s_t, a_t; \boldsymbol{w})\)和\(\hat{y}_t\)分别是价值网络在\(t\)时刻和\(t+m\)时刻做出的预测,两者都是对\(Q_\pi(s_t, a_t)\)的估计值。\(\hat{q}_t\)是纯粹的预测,而\(\hat{y}_t\)则基于\(m\)组实际观测,因此\(\hat{y}_t\)比\(\hat{q}_t\)更可靠。我们鼓励\(\hat{q}_t\)接近\(\hat{y}_t\)。设损失函数为:
\(L(\boldsymbol{w}) \triangleq \frac{1}{2} \Big[q(s_t, a_t; \boldsymbol{w}) - \hat{y}_t\Big]^2.\)
做一步梯度下降更新价值网络参数\(\boldsymbol{w}\):
\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot (\hat{q}_t - \hat{y}_t) \cdot \nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}).\)
训练流程:
设当前价值网络的参数为\(\boldsymbol{w}_{\text{now}}\), 当前策略为\(\pi_{\text{now}}\)。执行以下步骤更新价值网络和策略。
- 用策略网络\(\pi_{\text{now}}\)控制智能体与环境交互,完成一个回合,得到轨迹\(s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_n, a_n, r_n\).
- 对于所有的\(t = 1, \cdots, n-m\),
计算\(\hat{q}_t = q(s_t, a_t;
\boldsymbol{w}_{\text{now}})\).
3.对于所有的\(t = 1, \cdots, n-m\),计算多步 TD 目标和 TD 误差:
\(\hat{y}_t = \sum_{i=0}^{m-1} \gamma^i r_{t+i} + \gamma^m \hat{q}_{t+m}, \quad \delta_t = \hat{q}_t - \hat{y}_t.\)
- 对于所有的\(t = 1, \cdots, n-m\), 对价值网络\(q\)做反向传播,计算\(q\)关于\(\boldsymbol{w}\)的梯度:\(\nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}_{\text{now}})\).
- 更新价值网络参数:
\(\boldsymbol{w}_{\text{new}} \leftarrow \boldsymbol{w}_{\text{now}} - \alpha \cdot \sum_{t=1}^{n-m} \delta_t \cdot \nabla_{\boldsymbol{w}} q(s_t, a_t; \boldsymbol{w}_{\text{now}}).\)
- 用某种算法更新策略函数\(\pi\)。该算法与 SARSA 算法无关。
蒙特卡洛与自举
上一节介绍了多步 TD 目标。单步 TD 目标、回报是多步 TD 目标的两种特例。如下图所示,如果设\(m=1\),那么多步 TD 目标变成单步 TD 目标。如果设\(m=n-t+1\),那么多步 TD 目标变成实际观测的回报\(u_t\)。

蒙特卡洛
训练价值网络\(q(s, a; \boldsymbol{w})\)的时候,我们可以将一局游戏进行到底,观测到所有的奖励\(r_1, \cdots, r_n\),然后计算回报\(u_t = \sum_{i=0}^{n-t} \gamma^i r_{t+i}\)。拿\(u_t\)作为目标,鼓励价值网络\(q(s_t, a_t; \boldsymbol{w})\)接近\(u_t\)。定义损失函数:
\(L(\boldsymbol{w}) = \frac{1}{2} \left[q(s_t, a_t; \boldsymbol{w}) - u_t\right]^2.\)
然后做一次梯度下降更新\(\boldsymbol{w}\):
\(\boldsymbol{w} \leftarrow \boldsymbol{w} - \alpha \cdot \nabla_{\boldsymbol{w}} L(\boldsymbol{w}),\)
这样可以让价值网络的预测\(q(s_t, a_t; \boldsymbol{w})\)更接近\(u_t\)。这种训练价值网络的方法不是 TD。
在强化学习中,训练价值网络的时候以\(u_t\)作为目标,这种方式被称作“蒙特卡洛”。原因是这样的,动作价值函数可以写作\(Q_{\pi}(s_{t}, a_{t}) = \mathbb{E}[U_{t} \mid S_{t} = s_{t}, A_{t} = a_{t}].\), 而我们用实际观测\(u_t\)去近似期望,这就是典型的蒙特卡洛近似。
蒙特卡洛的好处是无偏性:\(u_t\)是\(Q_\pi(s_t, a_t)\)的无偏估计。由于\(u_t\)的无偏性,拿\(u_t\)作为目标训练价值网络,得到的价值网络也是无偏的。
蒙特卡洛的坏处是方差大。随机变量\(U_t\)依赖于\(S_{t+1}, A_{t+1}, \cdots, S_n, A_n\)这些随机变量,其中不确定性很大。观测值\(u_t\)虽然是\(U_t\)的无偏估计,但可能实际上离\(\mathbb{E}\{U_t\}\)很远。
因此,拿\(u_t\)作为目标训练价值网络,收敛会很慢。
自举
在介绍价值学习的自举之前,先解释一下什么叫自举。大家可能经常在强化学习和统计学的文章里见到 bootstrapping 这个词。它的字面意思是“拔自己的鞋带,把自己举起来”。所以 bootstrapping 翻译成“自举”, 即自己把自己举起来。自举听起来很荒谬。即使你“力拔山兮气盖世”,你也没办法拔自己的鞋带,把自己举起来。虽然自举乍看起来不现实,但是在统计和 机器学习 是可以做到自举的;自举在统计和机器学习里面非常常用。
在强化学习中,“自举”的意思是“用一个估算去更新同类的估算”,类似于“自己把自己给举起来”。SARSA 使用的单步 TD 目标定义为:
SARSA 鼓励\(q(s_t, a_t; \boldsymbol{w})\)接近\(\hat{y}_t\), 所以定义损失函数:
\(L(w) = \frac{1}{2} \left[q(s_t, a_t; \boldsymbol{w}) - \hat{y}_t\right]^2.\)
TD 目标\(\hat{y}_t\)的一部分是价值网络做出的估计\(\gamma \cdot q(s_{t+1}, a_{t+1}; \boldsymbol{w})\), 然后 SARSA 让\(q(s_t, a_t; \boldsymbol{w})\)去拟合\(\hat{y}_t\)。这就是用价值网络自己做出的估计去更新价值网络自己,这属于“自举”。(严格地说,TD 目标\(\hat{y}_t\)中既有自举的成分,也有蒙特卡洛的成分。TD 目标中的\(\gamma \cdot q(s_{t+1}, a_{t+1}; \boldsymbol{w})\)是自举,因为它拿价值网络自己的估计作为目标。TD 目标中的\(r_t\)是实际观测,它是对\(\mathbb{E}[R_t]\)的蒙特卡洛。)
自举的好处是方差小。单步 TD 目标的随机性只来自于\(S_{t+1}, A_{t+1}\), 而回报\(U_t\)的随机性来自于\(S_{t+1}, A_{t+1}, \cdots, S_n, A_n\)。很显然,单步 TD 目标的随机性较小,因此方差较小。用自举训练价值网络,收敛比较快。
自举的坏处是有偏差。价值网络\(q(s, a; \boldsymbol{w})\)是对动作价值\(Q_\pi(s, a)\)的近似。最理想的情况下,\(q(s, a; \boldsymbol{w}) = Q_\pi(s, a), \forall s, a\)。假如碰巧\(q(s_{j+1}, a_{j+1}; \boldsymbol{w})\)低估(或高估)真实价值\(Q_\pi(s_{j+1}, a_{j+1})\),则会发生下面的情况:
\(\begin{align*} &\Longrightarrow\quad q(s_{j+1}, a_{j+1}; w) \quad \text{低估(或高估)} \quad Q_{\pi}(s_{j+1}, a_{j+1}) \\ &\Longrightarrow\quad \widehat{y_{j}} \quad \text{低估(或高估)} \quad Q_{\pi}(s_{j}, a_{j}) \\ &\Longrightarrow\quad q(s_{j}, a_{j}; w) \quad \text{低估(或高估)} \quad Q_{\pi}(s_{j}, a_{j}). \end{align*}\)
也就是说,自举会让偏差从\((s_{t+1}, a_{t+1})\)传播到\((s_t, a_t)\)。后面详细讨论自举造成的偏差以及解决方案。
蒙特卡洛和自举的对比
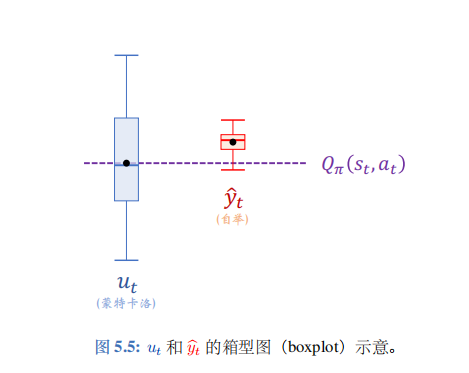
在价值学习中,用实际观测的回报\(u_t\)作为目标的方法被称为蒙特卡洛,即图 5.5 中的蓝色的箱型图。
\(u_t\)是\(Q_\pi(s_t, a_t)\)的无偏估计,即\(\mathbb{E}\{U_t\} = Q_\pi(s_t, a_t)\)。但是它的方差很大,也就是说实际观测到的\(u_t\)可能离\(Q_\pi(s_t, a_t)\)很远。
用单步 TD 目标\(\hat{y}_t\)作为目标的方法被称为自举,即图5.5 中的红色的箱型图。自举的好处在于方差小,\(\hat{y}_t\)不会偏离期望太远。但是\(\hat{y}_t\)往往是有偏的, 它的期望往往不等于\(Q_\pi(s_t, a_t)\)。用自举训练出的价值网络往往有系统性的偏差 (低估或者高估)。实践中,自举通常比蒙特卡洛收敛更快,这就是为什么训练 DQN 和价值网络通常用 TD 算法。
如图 5.4 所示,多步 TD 目标\(\hat{y}_t = \left(\sum_{i=0}^{m-1} \gamma^i r_{t+i}\right) + \gamma^m \cdot q(s_{t+m}, a_{t+m}; \boldsymbol{w})\)介于蒙特卡洛和自举之间。多步 TD 目标有很大的蒙特卡洛成分,其中的\(\sum_{i=0}^{m-1} \gamma^i r_{t+i}\)基于\(m\)个实际观测到的奖励。多步 TD 目标也有自举的成分,其中的\(\gamma^m \cdot q(s_{t+m}, a_{t+m}; \boldsymbol{w})\)是用价值网络自己算出来的。如果把\(m\)设置得比较好,可以在方差和偏差之间找到好的平衡,使得多步 TD 目标优于单步 TD 目标,也优于回报\(u_t\)。