5.1 经验回放

价值学习高级技巧

前面介绍了 DQN, 并且用 Q学习算法训练 DQN。如果用最原始的 Q 学习算法，那么训练出的 DQN 效果会很不理想。想要提升 DQN 的表现，需要用本章的高级技巧。文献中已经有充分实验结果表明这些高级技巧对 DQN 非常有效，而且这些技巧不冲突，可以一起使用。有些技巧并不局限于DQN，而是可以应用于多种价值学习和策略学习方法。

介绍经验回放 (experience replay) 和优先经验回放(prioritized experience replay)。讨论 DQN 的高估问题以及解决方案——目标网络(target network) 和双 Q 学习算法(double Q-learning)。

介绍两种方法改进 DQN 的神经网络结构 (不是对 Q 学习算法的改进)：对决网络 (dueling network),它把动作价值 (action value) 分解成状态价值(state value) 与优势 (advantage)；噪声网络 (noisy net), 它往神经网络的参数中加入随机噪声,鼓励探索。

经验回放

经验回放(experience replay)是强化学习中一个重要的技巧，可以大幅提升强化学习的表现。经验回放的意思是把智能体与环境交互的记录 (即经验) 储存到一个数组里，事后反复利用这些经验训练智能体。这个数组被称为经验回放数组 (replay buffer)。

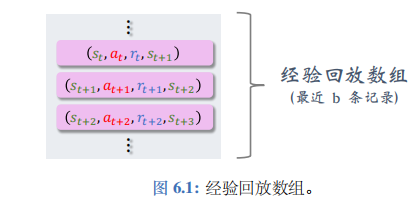
具体来说，把智能体的轨迹划分成\(s_t, a_t, r_t, s_{t+1}\)这样的四元组，存入一个数组。需要人为指定数组的大小 (记作\(b\))。数组中只保留最近\(b\)条数据；当数组存满之后，删除掉最旧的数据。数组的大小\(b\)是个需要调的超参数，会影响训练的结果。通常设置\(b\)为\(10^5\sim10^6\)。

在实践中，要等回放数组中有足够多的四元组时，才开始做经验回放更新 DQN。根据论文的实验分析，如果将 DQN 用于 Atari 游戏，最好是在收集到 20 万条四元组时才开始做经验回放更新 DQN; 如果是用更好的 Rainbow DQN, 收集到 8 万条四元组时就可以开始更新 DQN。在回放数组中的四元组数量不够的时候，DQN 只与环境交互，而不去更新 DQN 参数，否则实验效果不好。

经验回放的优点

经验回放的一个好处在于打破序列的相关性。训练 DQN 的时候，每次我们用一个四元组对 DQN 的参数做一次更新。我们希望相邻两次使用的四元组是独立的。然而当智能体收集经验的时候，相邻两个四元组\((s_t, a_t, r_t, s_{t+1})\)和\((s_{t+1}, a_{t+1}, r_{t+1}, s_{t+2})\)有很强的相关性。依次使用这些强关联的四元组训练 DQN, 效果往往会很差。经验回放每次从数组里随机抽取一个四元组，用来对 DQN 参数做一次更新。这样随机抽到的四元组都是独立的，消除了相关性。

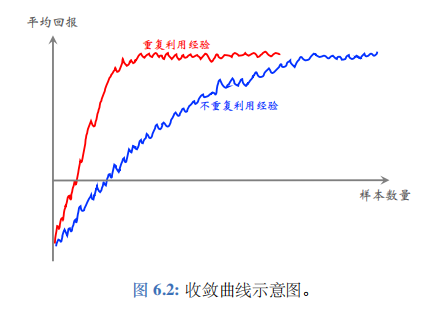
经验回放的另一个好处是重复利用收集到的经验、而不是用一次就丢弃，这样可以用更少的样本数量达到同样的表现。重复利用经验、不重复利用经验的收敛曲线通常如图 6.2 所示。图的横轴是样本数量，纵轴是平均回报。

注 在阅读文献的时候请注意“样本数量"(sample complexity) 与“更新次数"两者的区别。样本数量是指智能体从环境中获取的奖励\(r\)的数量。而一次更新的意思是从经验回放数组里取出一个或多个四元组，用它对参数\(w\)做一次更新。通常来说，样本数量更重要，因为在实际应用中收集经验比较困难。比如，在机器人的应用中，需要在现实世界做一次实验才能收集到一条经验，花费的时间和金钱远大于做一次计算。相对而言，做更新的次数不是那么重要，更新次数只会影响训练时的计算量而已。

经验回放的局限性

需要注意，并非所有的强化学习方法都允许重复使用过去的经验。经验回放数组里的数据全都是用行为策略 (behavior policy) 控制智能体收集到的。在收集经验同时，我们也在不断地改进策略。策略的变化导致收集经验时用的行为策略是过时的策略，不同于当前我们想要更新的策略——即目标策略(target policy)。也就是说，经验回放数组中的经验通常是过时的行为策略收集的，而我们真正想要学的目标策略不同于过时的行为策略。

有些强化学习方法允许行为策略不同于目标策略。这样的强化学习方法叫做异策略(off-policy)。比如 Q 学习、确定策略梯度 (DPG) 都属于异策略。由于它们允许行为策略不同于目标策略，过时的行为策略收集到的经验可以被重复利用。经验回放适用于异策略。

有些强化学习方法要求行为策略与目标策略必须相同。这样的强化学习方法叫做同策略 (on-policy)。比如 SARSA、REINFORCE、A2C 都属于同策略。它们要求经验必须是当前的目标策略收集到的，而不能使用过时的经验。经验回放不适用于同策略。

优先经验回放

优先经验回放 (prioritized experience replay) 是一种特殊的经验回放方法，它比普通的经验回放效果更好：既能让收敛更快，也能让收敛时的平均回报更高。经验回放数组里有\(b\)个四元组，普通经验回放每次均匀抽样得到一个样本——即四元组\((s_j, a_j, r_j, s_{j+1})\)。用它来更新 DQN 的参数。优先经验回放给每个四元组一个权重，然后根据权重做非均匀随机抽样。如果 DQN 对\((s_j, a_j)\)的价值判断不准确，即\(Q(s_j, a_j; w)\)离\(Q^*(s_j, a_j)\)较远，则四元组\((s_j, a_j, r_j, s_{j+1})\)应当有较高的权重。

为什么样本的重要性会有所不同呢？设想你用强化学习训练一辆无人车。经验回放数组中的样本绝大多数都是车辆正常行驶的情形，只有极少数样本是意外情况，比如旁边车辆强行变道、行人横穿马路、警察封路要求绕行。数组中的样本的重要性显然是不同的。绝大多数的样本都是车辆正常行驶，而且正常行驶的情形很容易处理，出错的可能性非常小。意外情况的样本非常少，但是又极其重要，处理不好就会车毁人亡。所以意外情况的样本应当有更高的权重，受到更多关注。这两种样本不应该同等对待。

如何自动判断哪些样本更重要呢？举个例子，自动驾驶中的意外情况数量少、而且难以处理，导致 DQN 的预测\(Q(s_j, a_j; w)\)严重偏离真实价值\(Q^*(s_j, a_j)\)。因此，要是\(|Q(s_j, a_j; w) - Q^*(s_j, a_j)|\)较大，则应该给样本\((s_j, a_j, r_j, s_{j+1})\)较高的权重。然而实际上我们不知道\(Q^*\)，因此无从得知\(|Q(s_j, a_j; w) - Q^*(s_j, a_j)|\)。不妨把它替换成 TD 误差。回忆一下，TD 误差的定义是：

\(\delta_j = \Delta Q(s_j, a_j; w_{\text{now}}) - [r_t + \gamma \cdot \max_a Q(s_{j+1}, a; w_{\text{now}})]\)

如果 TD 误差的绝对值\(|\delta_j|\)大，说明 DQN 对\((s_j, a_j)\)的真实价值的评估不准确，那么应该给\((s_j, a_j, r_j, s_{j+1})\)设置较高的权重。

优先经验回放对数组里的样本做非均匀抽样。四元组\((s_j, a_j, r_j, s_{j+1})\)的权重是 TD 误差的绝对值\(|\delta_j|\)。有两种方法设置抽样概率。一种抽样概率是：

\(p_j \propto |\delta_j| + \epsilon\).

此处的\(\epsilon\)是个很小的数，防止抽样概率接近零，用于保证所有样本都以非零的概率被抽到。另一种抽样方式先对\(|\delta_j|\)做降序排列，然后计算

\(p_j \propto \frac{1}{\text{rank}(j)}\).

此处的\(\text{rank}(j)\)是\(|\delta_j|\)的序号。大的\(|\delta_j|\)的序号小，小的\(|\delta_j|\)的序号大。两种方式的原理是一样的，\(|\delta_j|\)大的样本被抽样到的概率大。

优先经验回放做非均匀抽样，四元组\((s_j, a_j, r_j, s_{j+1})\)被抽到的概率是\(p_j\)。抽样是非均匀的，不同的样本有不同的抽样概率，这样会导致 DQN 的预测有偏差。应该相应调整学习率，抵消掉不同抽样概率造成的偏差。TD 算法用“随机梯度下降”来更新参数：

\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot g\),

此处的\(\alpha\)是学习率，\(g\)是损失函数关于\(w\)的梯度。如果用均匀抽样，那么所有样本有相同的学习率\(\alpha\)。如果做非均匀抽样的话，应该根据抽样概率来调整学习率\(\alpha\)。如果一条样本被抽样的概率大，那么它的学习率就应该比较小。可以这样设置学习率：

\(\alpha_j = \frac{\alpha}{(b \cdot p_j)^\beta}\),

此处的\(b\)是经验回放数组中样本的总数，\(\beta \in (0, 1)\)是个需要调的超参数（论文里建议一开始让\(\beta\)比较小，最终增长到 1）。

注 均匀抽样是一种特例，即所有抽样概率都相等：

\(p_1 = \cdots = p_b = \frac{1}{b}\).

在这种情况下，有\((b \cdot p_j)^\beta = 1\), 因此学习率都相同：

\(\alpha_1 = \cdots = \alpha_b = \alpha_o\).

注 读者可能会问下面的问题。如果样本\((s_j, a_j, r_j, s_{j+1})\)很重要，它被抽到的概率\(p_j\)很大，可是它的学习率却很小。当\(\beta = 1\)时，如果抽样概率\(p_j\)变大 10 倍，则学习率\(\alpha_j\)减小 10 倍。抽样概率、学习率两者岂不是抵消了吗，那么优先经验回放有什么意义呢？大抽样概率、小学习率两者其实并没有抵消，因为下面两种方式并不等价：

• 设置学习率为\(\alpha\),使用样本\((s_j, a_j, r_j, s_{j+1})\)计算一次梯度，更新一次参数\(w\);
• 设置学习率为\(\frac{\alpha}{10}\), 使用样本\((s_j, a_j, r_j, s_{j+1})\)计算十次梯度，更新十次参数\(w\)。

乍看起来两种方式区别不大，但其实第二种方式是对样本更有效的利用。第二种方式的缺点在于计算量大了十倍，所以第二种方式只被用于重要的样本。

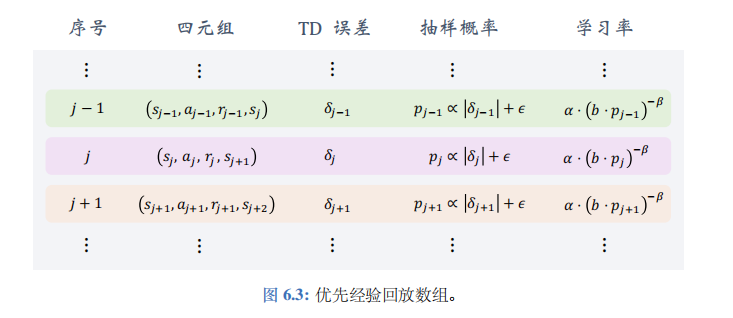
优先经验回放数组如图 6.3 所示。设\(b\)为数组大小，需要手动调整。如果样本 (即四元组) 的数量超过了\(b\),那么要删除最旧的样本。数组里记录了四元组、TD 误差、抽样概率、以及学习率。注意，数组里存的 TD 误差\(\delta_j\)是用很多步之前过时的 DQN 参数计算出来的：

\(\delta_j = Q(s_j, a_j; w_{\text{old}}) - [r_t + \gamma \cdot \max_a Q(s_{j+1}, a; w_{\text{old}})]\).

做经验回放的时候，每次取出一个四元组，用它计算出新的 TD 误差：

\(\delta_j' = Q(s_j, a_j; w_{\text{now}}) - [r_t + \gamma \cdot \max_a Q(s_{j+1}, a; w_{\text{now}})]\),

然后用它更新 DQN 的参数。用这个新的\(\delta_j'\)取代数组中旧的\(\delta_j\)。