5.2 高估问题

高估问题及解决方法

Q 学习算法有一个缺陷：用 Q 学习训练出的 DQN 会高估真实的价值，而且高估通常是非均匀的。这个缺陷导致 DQN 的表现很差。高估问题并不是 DQN 模型的缺陷，而是 Q 学习算法的缺陷。

Q 学习产生高估的原因有两个：第一，自举导致偏差的传播；第二，最大化导致 TD 目标高估真实价值。为了缓解高估，需要从导致高估的两个原因下手，改进 Q学习算法。双 Q学习算法是一种有效的改进，可以大幅缓解高估及其危害。

自举导致偏差的传播

在强化学习中，自举意思是“用一个估算去更新同类的估算”,类似于“自己把自己给举起来”。我们在前面的笔记中讨论过 SARSA 算法中的自举。下面回顾训练 DQN 用的 Q学习算法，研究其中存在的自举。算法每次从经验回放数组中抽取一个四元组\((s_j, a_j, r_j, s_{j+1})\)。然后执行以下步骤，对 DQN 的参数做一轮更新：

1.计算TD目标：

\(y_j^{\hat{}} = r_j + \gamma \cdot \max_a Q(s_{j+1}, a; w_{\text{now}})\)

2.定义损失函数

\(L(w) = \frac{1}{2} [Q(s_j, a_j; w) - y_j^{\hat{}}]^2\)

3.把\(y_j^{\hat{}}\)看做常数，做一次梯度下降更新参数：

\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \nabla_w L(w_{\text{now}})\)

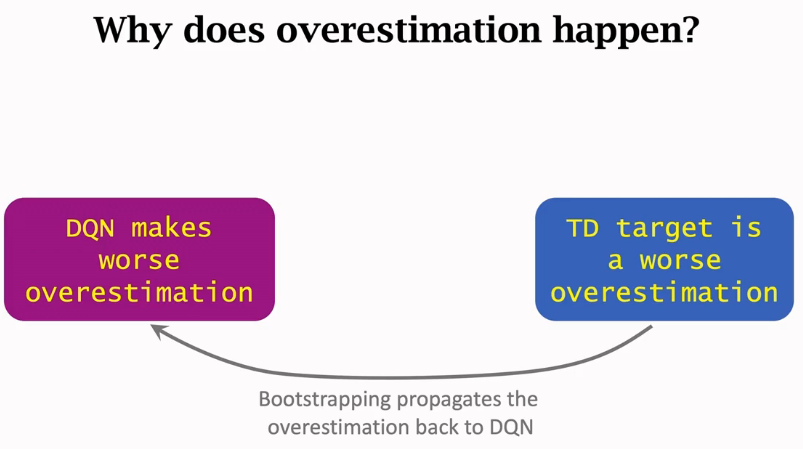
第一步中的 TD 目标\(y_j^{\hat{}}\)部分基于 DQN 自己做出的估计。第二步让 DQN 去拟合\(y_j^{\hat{}}\)。这就意味着我们用了 DQN 自己做出的估计去更新 DQN 自己，这属于自举。

自举对 DQN 的训练有什么影响呢？

\(Q(s, a; w)\)是对价值\(Q^*(s, a)\)的近似，最理想的情况下，\(Q(s, a; w) = Q^*(s, a)\)，\(\forall s, a\)。假如碰巧\(Q(s_{j+1}, a_{j+1}; w)\)低估(或高估)真实价值\(Q^*(s_{j+1}, a_{j+1})\), 则会发生下面的情况：

\(\begin{align*} Q(s_{j+1}, a_{j+1}; w) & \quad \text{低估(或高估)} \quad Q^*(s_{j+1}, a_{j+1}) \\ \implies \widehat{y}_j & \quad \text{低估(或高估)} \quad Q^*(s_j, a_j) \\ \implies Q(s_j, a_j; w) & \quad \text{低估(或高估)} \quad Q^*(s_j, a_j). \end{align*}\)

如果\(Q(s_{j+1},a_{j+1};\boldsymbol{w})\)是对真实价值\(Q_\star(s_{j+1},a_{j+1})\)的低估 (或高估), 就会导致\(Q(s_j,a_j;\boldsymbol{w})\)低估 (或高估) 价值\(Q_\star(s_j,a_j)\),也就是说低估 (或高估) 从\((s_{j+1},a_{j+1})\)传播到\((s_j,a_j)\), 让更多的价值被低估 (或高估)。

最大化导致高估

首先用数学解释为什么最大化会导致高估。设\(x_1, \cdots, x_d\)为任意\(d\)个实数。往\(x_1, \cdots, x_d\)中加入任意均值为零的随机噪声，得到\(Z_1, \cdots, Z_d\),它们是随机变量，随机性来源于随机噪声。很容易证明均值为零的随机噪声不会影响均值：

\(\mathbb{E}[mean(Z_1, \cdots, Z_d)] = mean(x_1, \cdots, x_d)\).

用稍微复杂一点的证明，可以得到：

\(\mathbb{E}[max(Z_1, \cdots, Z_d)] \geq max(x_1, \cdots, x_d)\).

\(E[max(Z1,⋯,Zd)]≥max(x1,⋯,xd).\)

公式中的期望是关于噪声求的。这个不等式意味着先加入均值为零的噪声，然后求最大值，会产生高估。

假设对于所有的动作\(a \in A\)和状态\(s \in S\), DQN 的输出是真实价值\(Q^*(s, a)\)加上均值为零的随机噪声\(\epsilon\):

\(Q(s, a; w) = Q^*(s, a) + \epsilon\).

显然\(Q(s, a; w)\)是对真实价值\(Q^*(s, a)\)的无偏估计。然而有这个不等式：

\(\mathbb{E}_{\epsilon} \left[ \max_{a \in \mathcal{A}} Q(s, a; w) \right] \geq \max_{a \in \mathcal{A}} Q^{\star}(s, a).\)

公式说明哪怕 DQN 是对真实价值的无偏估计，但是如果求最大化，DQN 就会高估真实价值。复习一下，TD 目标是这样算出来的：

\(\widehat{y}_{j} = r_{j} + \gamma \cdot \underbrace{\max_{a \in \mathcal{A}} Q\left(s_{j+1}, a; w\right)}_{\text{高估} \max_{a \in \mathcal{A}} Q^{\star}\left(s_{j+1}, a\right)}.\)

这说明 TD 目标\(y_j^{\hat{}}\)通常是对真实价值\(Q^*(s_j, a_j)\)的高估。TD 算法鼓励\(Q(s_j, a_j; w)\)接近 TD 目标\(y_j^{\hat{}}\), 这会导致\(Q(s_j, a_j; w)\)高估真实价值\(Q^*(s_j, a_j)\)。

即使 DQN 是真实价值\(Q^*\)的无偏估计，只要 DQN 不恒等于\(Q^*\), TD 目标就会高估真实价值。TD 目标是高估，而 Q学习算法鼓励 DQN 预测接近 TD 目标，因此 DQN 会出现高估。

高估的危害

我们为什么要避免高估？高估真的有害吗？如果高估是均匀的，则高估没有危害；如果高估非均匀，就会有危害。举个例子，动作空间是\(A = \{左，右，上\}\)。给定当前状态\(s\), 每个动作有一个真实价值：

\(Q^*(s, 左) = 200, Q^*(s, 右) = 100, Q^*(s, 上) = 230\).

智能体应当选择动作“上”,因为“上”的价值最高。假如高估是均匀的，所有的价值都被高估了100：

\(Q(s, 左; w) = 300, Q(s, 右; w) = 200, Q(s, 上; w) = 330\).

那么动作“上”仍然有最大的价值，智能体会选择“上”。这个例子说明高估本身不是问题， 只要所有动作价值被同等高估。

但实践中，所有的动作价值会被同等高估吗？每当取出一个四元组\((s, a, r, s')\)用来更新一次 DQN, 就很有可能加重 DQN 对\(Q^*(s, a)\)的高估。对于同一个状态\(s\), 三种组合\((s, 左)\)、\((s, 右)\)、\((s, 上)\)出现在经验回放数组中的频率是不同的，所以三种动作被高估的程度是不同的。假如动作价值被高估的程度不同，比如

\(Q(s, 左; w) = 280, Q(s, 右; w) = 300, Q(s, 上; w) = 260\),

那么智能体做出的决策就是向右走，因为“右”的价值貌似最高。但实际上“右”是最差的动作，它的实际价值低于其余两个动作。

综上所述，用 Q学习算法训练 DQN 总会导致 DQN 高估真实价值。对于多数的\(s \in S\)和\(a \in A\), 有这样的不等式：

\(Q(s, a; w) > Q^*(s, a)\).

高估本身不是问题，真正的麻烦在于 DQN 的高估往往是非均匀的。如果 DQN 有非均匀的高估，那么用 DQN 做出的决策是不可靠的。我们已经分析过导致高估的原因：

• TD 算法属于“自举”,即用 DQN 的估计值去更新 DQN 自己。自举会导致偏差的传播。如果\(Q(s_{j+1}, a_{j+1}; w)\)是对\(Q^*(s_{j+1}, a_{j+1})\)的高估，那么高估会传播到\((s_j, a_j)\)让\(Q(s_j, a_j; w)\)高估\(Q^*(s_j, a_j)\)。自举导致 DQN 的高估从一个二元组\((s, a)\)传播到更多的二元组。
• TD 目标\(y_j^{\hat{}}\)中包含一项最大化，这会导致 TD 目标高估真实价值\(Q_*\)。Q 学习算法鼓励 DQN 的预测接近 TD 目标，因此 DQN 会高估\(Q_*\)。

找到了产生高估的原因，就可以想办法解决问题。想要避免 DQN 的高估，要么切断自举，要么避免最大化造成高估。注意，高估并不是 DQN 自身的属性，高估纯粹是算法造成的。想要避免高估，就要用更好的算法替代原始的 Q 学习算法。

使用目标网络

上文已经讨论过，切断“自举”可以避免偏差的传播，从而缓解 DQN 的高估。回顾一下，Q 学习算法这样计算 TD 目标：

\(\widehat{y}_j = r_j + \gamma \cdot \max_{a \in \mathcal{A}} Q(s_{j+1}, a; w) \,.\)

然后做梯度下降更新\(w\),使得\(Q(s_j, a_j; w)\)更接近\(y_j^{\hat{}}\)。想要切断自举，可以用另一个神经网络计算 TD 目标，而不是用 DQN 自己计算 TD 目标。另一个神经网络被称作 目标网络 (target network) 。把目标网络记作：

\(Q(s, a; w^-)\).

它的神经网络结构与 DQN 完全相同，但是参数\(w^-\)不同于\(w\)。

使用目标网络的话，Q 学习算法用下面的方式实现。每次随机从经验回放数组中取一个四元组，记作\((s_j, a_j, r_j, s_{j+1})\)。设 DQN 和目标网络当前的参数分别为\(w_{\text{now}}\)和\(\bar{w}_{\text{now}}\), 执行下面的步骤对参数做一次更新：

1.对 DQN 做正向传播，得到：

\(q_j^{\hat{}} = Q(s_j, a_j; w_{\text{now}})\)

2.对目标网络做正向传播，得到

\(q_{j+1}^{-} = \max_a Q(s_{j+1}, a; w_{\text{now}}^-)\)

3.计算 TD 目标和 TD 误差：

\(y_j^- = r_j + \gamma \cdot q_{j+1}^{-}\)和\(\delta_j = q_j^{\hat{}} - y_j^-\)

4.对 DQN 做反向传播，得到梯度

\(\nabla_w Q(s_j, a_j; w_{\text{now}})\)

5.做梯度下降更新 DQN 的参数：

\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \delta_j \cdot \nabla_w Q(s_j, a_j; w_{\text{now}})\)

6.设\(\tau \in (0, 1)\)是需要手动调的超参数。做加权平均更新目标网络的参数：

\(\bar{w}_{\text{new}} \leftarrow \tau \cdot w_{\text{new}} + (1 - \tau) \cdot \bar{w}_{\text{now}}\)

如图 6.4 (左) 所示，原始的 Q学习算法用 DQN 计算\(y_j^{\hat{}}\),然后拿\(y_j^{\hat{}}\)更新 DQN 自己， 造成自举。如图 6.4(右)所示，可以改用目标网络计算\(y_j^{\hat{}}\),这样就避免了用 DQN 的估计更新 DQN 自己，降低自举造成的危害。然而这种方法不能完全避免自举，原因是目标网络的参数仍然与 DQN 相关。

双 Q 学习算法

造成 DQN 高估的原因不是 DQN 模型本身的缺陷，而是 Q 学习算法有不足之处：第一，自举造成偏差的传播；第二，最大化造成 TD 目标的高估。在 Q 学习算法中使用目标网络，可以缓解自举造成的偏差，但是无助于缓解最大化造成的高估。本小节介绍双 Q 学习 (double Q learning) 算法，它在目标网络的基础上做改进，缓解最大化造成的高估。

注 本小节介绍的双 Q 学习算法在文献中被称作 double DQN, 缩写 DDQN。本书不采用 DDQN这名字，因为这个名字比较误导。双 Q 学习 (即所谓的 DDQN) 只是一种 TD 算法而已，它可以把 DQN 训练得更好。双 Q 学习并没有用区别于 DQN 的模型。本节中的模型只有一个，就是 DQN。我们讨论的只是训练 DQN 的三种 TD 算法：原始的 Q 学习、 用目标网络的 Q 学习、双 Q 学习。

为了解释原始的 Q 学习、用目标网络的 Q 学习、以及双 Q 学习三者的区别，我们再回顾一下Q 学习算法中的 TD 目标：

\(\widehat{y}_j = r_j + \gamma \cdot \max_{a \in \mathcal{A}} Q(s_{j+1}, a; w) \,.\)

不妨把最大化拆成两步：

1.选择——即基于状态\(s_{j+1}\),选出一个动作使得 DQN 的输出最大化：

\(a^{\star} = \underset{a \in A}{\operatorname{argmax}} Q(s_{j+1}, a; w)\)

2.求值——即计算\((s_{j+1}, a^{\star})\)的价值，从而算出 TD 目标：

\(y_j^{\hat{}} = r_j + Q(s_{j+1}, a^{\star}; w)\)

以上是原始的 Q 学习算法，选择和求值都用 DQN。上一小节改进了 Q 学习，选择和求值都用目标网络：

选择：

\(a^- = \underset{a \in A}{\operatorname{argmax}} Q(s_{j+1}, a; w^-)\),

求值：

\(\widetilde{y}_j = r_j + Q(s_{j+1}, a^-; w^-)\).

本小节介绍双 Q 学习，第一步的选择用 DQN, 第二步的求值用目标网络：

选择：

\(a^{\star} = \underset{a \in A}{\operatorname{argmax}} Q(s_{j+1}, a; w)\),

求值：

\(\widetilde{y}_j = r_j + Q(s_{j+1}, a^{\star}; w^-)\).

为什么双 Q 学习可以缓解最大化造成的高估呢？不难证明出这个不等式：

\(\underbrace{Q\left(s_{j+1}, a^{*}; w^{-}\right)}_{\text{双 Q学习}} \leq \underbrace{\max_{a \in \mathcal{A}} Q\left(s_{j+1}, a; w^{-}\right)}_{\text{用目标网络的 Q学习}}.\).

因此，

\(\underbrace{\widetilde{y}_{t}}_{\text{双Q学习}} \leq \underbrace{\widehat{y}_{t}}_{\text{用目标网络的Q学习}}.\)

这个公式说明双 Q 学习得到的 TD 目标更小。也就是说，与用目标网络的 Q 学习相比，双 Q学习缓解了高估。

双 Q 学习算法的流程如下。每次随机从经验回放数组中取出一个四元组，记作\((s_j, a_j, r_j, s_{j+1})\)。设 DQN 和目标网络当前的参数分别为\(w_{\text{now}}\)和\(w_{\text{now}}^-\), 执行下面的步骤对参数做一次更新：

1.对 DQN 做正向传播，得到：

\(q_j^{\hat{}} = Q(s_j, a_j; w_{\text{now}})\)

2.选择：

\(a^{\star} = \underset{a \in A}{\operatorname{argmax}} Q(s_{j+1}, a; w_{\text{now}})\)

3.求值：

\(q_{j+1} = Q(s_{j+1}, a^{\star}; \bar{w}_{\text{now}})\)

4.计算 TD 目标和 TD 误差：

\(\widetilde{y}_j = r_j + \gamma \cdot q_{j+1}\)和\(\delta_j = q_j^{\hat{}} - \widetilde{y}_j\)

5.对 DQN 做反向传播，得到梯度

\(\nabla_w Q(s_j, a_j; w_{\text{now}})\)

6.做梯度下降更新 DQN 的参数：

\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \delta_j \cdot \nabla_w Q(s_j, a_j; w_{\text{now}})\)

7.设\(\tau \in (0, 1)\)是需要手动调整的超参数。做加权平均更新目标网络的参数：

\(\bar{w}_{\text{new}} \leftarrow \tau \cdot w_{\text{new}} + (1 - \tau) \cdot \bar{w}_{\text{now}}\)

总结

本节研究了 DQN 的高估问题以及解决方案。DQN 的高估不是 DQN 模型造成的，不是 DQN 的本质属性。高估只是因为原始 Q 学习算法不好。Q 学习算法产生高估的原因有两个：第一，自举导致偏差从一个\((s, a)\)二元组传播到更多的二元组；第二，最大化造成 TD 目标高估真实价值。

想要解决高估问题，就要从自举、最大化这两方面下手。本节介绍了两种缓解高估的算法：使用目标网络、双Q 学习。Q 学习算法与目标网络的结合可以缓解自举造成的偏差。双 Q学习基于目标网络的想法，进一步将 TD 目标的计算分解成选择和求值两步， 缓解了最大化造成的高估。图 6.5 总结了本节研究的三种算法。

注 如果使用原始 Q 学习算法，自举和最大化都会造成严重高估。在实践中，应当尽量使用双 Q学习，它是三种算法中最好的。

注 如果使用 SARSA 算法 (比如在 actor-critic 中), 自举的问题依然存在，但是不存在最大化造成高估这一问题。对于 SARSA, 只需要解决自举问题，所以应当将目标网络应用到 SARSA 。