5.3 Dueling Network
对决网络 (Dueling Network)
本节介绍对决网络 (dueling network), 它是对 DQN 的神经网络结构的改进。它的基本想法是将最优动作价值\(Q^*\)分解成最优状态价值\(V^*\)加最优优势\(D^*\)。对决网络的训练与 DQN 完全相同,可以用 Q 学习算法或者双 Q 学习算法 。
最优优势函数
在介绍对决网络 (dueling network)之前,先复习一些基础知识。动作价值函数\(Q_\pi(s, a)\)是回报的期望:
\(Q_\pi(s, a) = \mathbb{E}[U_t | S_t = s, A_t = a]\).
最优动作价值\(Q^*\)的定义是:
\(Q^*(s, a) = \max_\pi Q_\pi(s, a), \forall s \in S, a \in A\).
状态价值函数\(V_\pi(s)\)是\(Q_\pi(s, a)\)关于\(a\)的期望:
\(V_\pi(s) = \mathbb{E}_{A \sim \pi}[Q_\pi(s, A)]\).
最优状态价值\(V^*\)的定义是:
\(V^*(s) = \max_\pi V_\pi(s), \forall s \in S\).
最优优势函数 (optimal advantage function) 的定义是:
\(D^*(s, a) \triangleq Q^*(s, a) - V^*(s)\).
通过数学推导,可以证明下面的定理:

\(Q^*(s, a) = V^*(s) + D^*(s, a) - \max_a D^*(s, a) \quad \forall s \in S, a \in A\).
对决网络
与 DQN 一样,对决网络 (dueling network) 也是对最优动作价值函数\(Q^*\)的近似。对决网络与 DQN 的区别在于神经网络结构不同。直观上,对决网络可以了解到哪些状态有价值或者没价值,而无需了解每个动作对每个状态的影响。实践中,对决网络具有更好的效果。由于对决网络与 DQN 都是对\(Q^*\)的近似,可以用完全相同的算法训练两种神经网络。
对决网络由两个神经网络组成。一个神经网络记作\(D(s, a; w^D)\), 它是对最优优势函数\(D^*(s, a)\)的近似。另一个神经网络记作\(V(s; w^V)\),它是对最优状态价值函数\(V^*(s)\)的近似。把定理 6.1 中的\(D^*\)和\(V^*\)替换成相应的神经网络,那么最优动作价值函数\(Q^*\)就被近似成下面的神经网络:
\(Q(s, a; w) \triangleq V(s; w^V) + D(s, a; w^D) - \max_{a \in \mathcal{A}} D(s, a; w^D).\).
公式左边的\(Q(s, a; w)\)就是对决网络,它是对最优动作价值函数\(Q^*\)的近似。它的参数记作\(w \triangleq (w^V; w^D)\)。
对决网络的结构如图 6.6 所示。
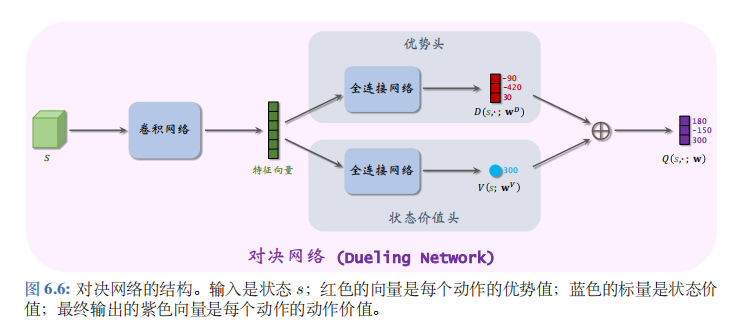
可以让两个神经网络\(D(s, a; w^D)\)与\(V(s; w^V)\)共享部分卷积层;这些卷积层把输入的状态\(s\)映射成特征向量,特征向量是“优势头”与“状态价值头”的输入。优势头输出一个向量,向量的维度是动作空间的大小\(\|A\|\), 向量每个元素对应一个动作。举个例子,动作空间是\(\{左,右,上\}\)。优势头的输出是三个值:
\(D(s, 左; w^D) = -90, D(s, 右; w^D) = -420, D(s, 上; w^D) = 30\).
状态价值头输出的是一个实数,比如
\(V(s; w^V) = 300\).
首先计算
\(\max_a D(s, a; w^D) = \max\{-90, -420, 30\} = 30\).
然后用公式 (6.1) 计算出:
\(Q(s, 左; w) = 180, Q(s, 右; w) = -150, Q(s, 上; w) = 300\).
这样就得到了对决网络的最终输出。
解决不唯一性
读者可能会有下面的疑问。对决网络是由定理 6.1 推导出的,而定理中最右的一项恒等于零:
\(\max_a D^*(s, a) = 0, \forall s \in S\).
也就是说,可以把最优动作价值写成两种等价形式:
\(\begin{array}{lll} Q_{\star}(s, a) &=& V_{\star}(s) + D_{\star}(s, a) & \text{(第一种形式)} \\ &=& V_{\star}(s) + D_{\star}(s, a) - \max_{a \in \mathcal{A}} D_{\star}(s, a). & \text{(第二种形式)} \end{array}\)
之前我们根据第二种形式实现对决网络。我们可否根据第一种形式,把对决网络按照下面的方式实现呢:
\(Q(s, a; w) = V(s; w^V) + D(s, a; w^D)\)?
答案是不可以这样实现对决网络,因为这样会导致不唯一性。假如这样实现对决网络,那么\(V\)和\(D\)可以随意上下波动,比如一个增大 100, 另一个减小 100:
\(V(s; w^{\tilde{V}}) \triangleq V(s; w^V) + 100, D(s, a; w^{\tilde{D}}) \triangleq D(s, a; w^D) - 100\).
这样的上下波动不影响最终的输出:
\(V(s; w^V) + D(s, a; w^D) = V(s; w^{\tilde{V}}) + D(s, a; w^{\tilde{D}})\).
这就意味着\(V\)和\(D\)的参数可以很随意地变化,却不会影响输出的 Q。我们不希望这种情况出现,因为这会导致训练的过程中参数不稳定。
因此很有必要在对决网络中加入\(\max_a D(s, a; w^D)\)这一项。它使得\(V\)和\(D\)不能随意上下波动。假如让\(V\)变大 100,让\(D\)变小 100, 则对决网络的输出会增大 100,而非不变:
\(V\left(s; \tilde{w}^{V}\right) + D\left(s, a; \tilde{w}^{D}\right) - \max_{a} D\left(s, a; \tilde{w}^{D}\right)\).
\(= V\left(s; w^{V}\right) + D\left(s, a; w^{D}\right) - \max_{a} D\left(s, a; w^{D}\right) + 100.\)
以上讨论说明了为什么\(\max_a D(s, a; w^D)\)这一项不能省略。
对决网络的实际实现
按照定理 6.1, 对决网络应该定义成:
\(Q(s, a; w) \triangleq V(s; w^V) + D(s, a; w^D) - \max_a D(s, a; w^D)\).
最右边的 max 项的目的是解决不唯一性。实际实现的时候,用 mean 代替 max 会有更好的效果。所以实际 上会这样定义对决网络:
\(Q(s, a; w) \triangleq V(s; w^V) + D(s, a; w^D) - \text{mean}_{a \in \mathcal{A}} D(s, a; w^D).\).
对决网络与 DQN 都是对最优动作价值函数\(Q^*\)的近似,所以对决网络的训练和决策与 DQN 完全一样。比如可以这样训练对决网络:
- 用\(\epsilon\)-greedy 算法控制智能体,收集经验,把\((s_j, a_j, r_j, s_{j+1})\)这样的四元组存入经验回放数组。
- 从数组里随机抽取四元组,用双 Q 学习算法更新对决网络参数\(w = (w^D, w^V)\)。
完成训练之后,基于当前状态\(s_t\),让对决网络给所有动作打分,然后选择分数最高的动作:
\(a_t = \underset{a \in A}{\operatorname{argmax}} Q(s_t, a; w)\).
简而言之,怎么样训练 DQN,就怎么样训练对决网络;怎么样用 DQN 做控制,就怎么样用对决网络做控制。如果一个技巧能改进 DQN 的训练,这个技巧也能改进对决网络。同样的道理,因为 Q 学习算法导致 DQN 出现高估,所以 Q 学习算法也会导致对决网络出现高估。
噪声网络
本节介绍噪声网络(noisy net),这是一种非常简单的方法,可以显著提高 DQN 的表现。噪声网络的应用不局限于 DQN, 它可以用于几乎所有的深度强化学习方法。
噪声网络的原理
把神经网络中的参数\(w\)替换成\(\mu + \sigma \circ \xi\)。此处的\(\mu\)、\(\sigma\)、\(\xi\)的形状与\(w\)完全相同。
\(\mu\)、\(\sigma\)分别表示均值和标准差,它们是神经网络的参数,需要从经验中学习。\(\xi\)是随机噪声,它的每个元素独立从标准正态分布\(\mathcal{N}(0,1)\)中随机抽取。符号“\(\circ\)”表示逐项乘积。
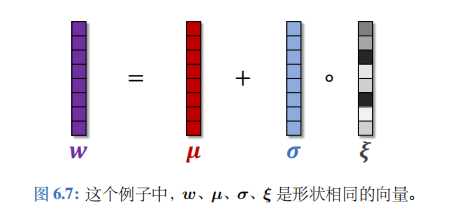
如果\(w\)是向量,那么有
\(w_i = \mu_i + \sigma_i \cdot \xi_i\).
如果\(w\)是矩阵,那么有
\(w_{ij} = \mu_{ij} + \sigma_{ij} \cdot \xi_{ij}\).
噪声网络的意思是参数\(w\)的每个元素\(w_i\)从均值为\(\mu_i\)、标准差为\(\sigma_i\)的正态分布中抽取。
举个例子,某一个全连接层记作:
\(z = \text{ReLU}(Wx + b)\).
公式中的向量\(x\)是输入,矩阵\(W\)和向量\(b\)是参数,ReLU 是激活函数,\(z\)是这一层的输出。噪声网络把这个全连接层替换成:
\(z = \text{ReLU}((W^\mu + W^\sigma \circ W^\xi)x + (b^\mu + b^\sigma \circ b^\xi))\).
公式中的\(W^\mu\)、\(W^\sigma\)、\(b^\mu\)、\(b^\sigma\)是参数,需要从经验中学习。矩阵\(W^\xi\)和向量\(b^\xi\)的每个元素都是独立从\(\mathcal{N}(0,1)\)中随机抽取的,表示噪声。
训练噪声网络的方法与训练标准的神经网络完全相同,都是做反向传播计算梯度,然后用梯度更新神经参数。把损失函数记作\(L\)。已知梯度\(\frac{\partial L}{\partial z}\),可以用链式法则算出损失关于参数的梯度:
\(\frac{\partial L}{\partial W^\mu} = \frac{\partial z}{\partial W^\mu} \cdot \frac{\partial L}{\partial z}, \frac{\partial L}{\partial b^\mu} = \frac{\partial z}{\partial b^\mu} \cdot \frac{\partial L}{\partial z}, \frac{\partial L}{\partial W^\sigma} = \frac{\partial z}{\partial W^\sigma} \cdot \frac{\partial L}{\partial z}, \frac{\partial L}{\partial b^\sigma} = \frac{\partial z}{\partial b^\sigma} \cdot \frac{\partial L}{\partial z}\).
然后可以做梯度下降更新参数\(W^\mu\)、\(W^\sigma\)、\(b^\mu\)、\(b^\sigma\)。
噪声 DQN
噪声网络可以用于 DQN。标准的 DQN 记作\(Q(s, a; w)\), 其中的\(w\)表示参数。把\(w\)替换成\(\mu + \sigma \circ \xi\), 得到噪声 DQN, 记作:
\(\tilde{Q}(s, a, \xi; \mu, \sigma) \triangleq Q(s, a; \mu + \sigma \circ \xi)\).
其中的\(\mu\)和\(\sigma\)是参数,一开始随机初始化,然后从经验中学习;而\(\xi\)则是随机生成,每个元素都从\(\mathcal{N}(0, 1)\)中抽取。噪声 DQN 的参数数量比标准 DQN 多一倍。
收集经验:
DQN 属于异策略 (off-policy)。我们用任意的行为策略 (behavior policy) 控制智能体,收集经验,事后做经验回放更新参数。在之前章节中,我们用\(\epsilon\)-greedy 作为行为策略:
\(a_t = \begin{cases} \underset{a \in A}{\operatorname{argmax}} Q(s_t, a; w), & \text{以概率 } (1-\epsilon); \\ \text{均匀抽取 } A \text{ 中的一个动作}, & \text{以概率 } \epsilon. \end{cases}\)
\(\epsilon\)-greedy 策略带有一定的随机性,可以让智能体尝试更多动作,探索更多状态。
噪声 DQN 本身就带有随机性,可以鼓励探索,起到与\(\epsilon\)-greedy 策略相同的作用。我们直接用
\(a_t = \underset{a \in A}{\operatorname{argmax}} \tilde{Q}(s, a, \xi; \mu, \sigma)\)
作为行为策略,效果比\(\epsilon\)-greedy 更好。每做一个决策,要重新随机生成一个\(\xi\)。
Q 学习算法:
训练的时候,每一轮从经验回放数组中随机抽样出一个四元组,记作\((s_j, a_j, r_j, s_{j+1})\)。从标准正态分布中做抽样,得到\(\xi'\)的每一个元素。计算 TD 目标:
\(\widehat{y}_j = r_j + \gamma \cdot \max_a \tilde{Q}(s_{j+1}, a, \xi'; \mu, \sigma)\).
把损失函数记作:
\(L(\mu, \sigma) = \frac{1}{2} [\tilde{Q}(s_j, a_j, \xi; \mu, \sigma) - \widehat{y}_j]^2\),
其中的\(\xi\)也是随机生成的噪声,但是它与\(\xi'\)不同。然后做梯度下降更新参数:
\(\mu \leftarrow \mu - \alpha_\mu \cdot \nabla_\mu L(\mu, \sigma), \sigma \leftarrow \sigma - \alpha_\sigma \cdot \nabla_\sigma L(\mu, \sigma)\).
公式中的\(\alpha_\mu\)和\(\alpha_\sigma\)是学习率。这样做梯度下降更新参数,可以让损失函数减小,让噪声 DQN 的预测更接近 TD 目标。
做决策 :
做完训练之后,可以用噪声 DQN 做决策。做决策的时候不再需要噪声,因此可以把参数\(\sigma\)设置成全零,只保留参数\(\mu\)。这样一来,噪声 DQN 就变成标准的 DQN:
\(\tilde{Q}(s, a, \xi'; \mu, 0) = Q(s, a; \mu)\).
在训练的时候往 DQN 的参数中加入噪声,不仅有利于探索,还能增强鲁棒性。鲁棒性的意思是即使参数被扰动,DQN 也能对动作价值\(Q^*\)做出可靠的估计。为什么噪声可以让 DQN 有更强的鲁棒性呢?
假设在训练的过程中不加入噪声。把学出的参数记作\(\mu\)。当参数严格等于\(\mu\)的时候 DQN 可以对最优动作价值做出较为准确的估计。但是对\(\mu\)做较小的扰动,就可能会让 DQN 的输出偏离很远。所谓“失之毫厘,谬以千里”。
噪声 DQN 训练的过程中,参数带有噪声:
\(w = \mu + \sigma \circ \xi\).
训练迫使 DQN 在参数带噪声的情况下最小化 TD 误差,也就是迫使 DQN 容忍对参数的扰动。训练出的 DQN 具有鲁棒性:参数不严格等于\(\mu\)也没关系,只要参数在\(\mu\)的邻域内,DQN 做出的预测都应该比较合理。用噪声 DQN, 不会出现“失之毫厘,谬以千里”。
训练流程
实际编程实现 DQN 的时候,应该将本章的四种技巧——优先经验回放、双 Q学习、对决网络、噪声 DQN——全部用到。应该用对决网络的神经网络结构,而不是简单的 DQN 结构。往对决网络中的参数\(w\)中加入噪声,得到噪声 DQN, 记作\(\tilde{Q}(s, a, \xi; \mu, \sigma)\)。训练要用双 Q学习、优先经验回放,而不是原始的 Q 学习。双 Q学习需要目标网络\(\tilde{Q}(s, a, \xi; \mu^-, \sigma^-)\)计算 TD 目标。它跟噪声 DQN 的结构相同,但是参数不同。
初始化的时候,随机初始化\(\mu\)、\(\sigma\),并且把它们赋值给目标网络参数:
\(\mu^- \leftarrow \mu. \sigma^- \leftarrow \sigma\).
然后重复下面的步骤更新参数。把当前的参数记作\(\mu_{\text{now}}\)、\(\sigma_{\text{now}}\)、\(\mu_{\text{now}}^-\)、\(\sigma_{\text{now}}^-\).
- 用优先经验回放,从数组中抽取一个四元组,记作\((s_j, a_j, r_j, s_{j+1})\)。
- 用标准正态分布生成\(\xi\)。对噪声 DQN 做正向传播,得到:
\(\widehat{q}_j = \tilde{Q}(s_j, a_j, \xi; \mu_{\text{now}}, \sigma_{\text{now}})\).
- 用噪声 DQN 选出最优动作:
\(\tilde{a}_{j+1} = \underset{a \in A}{\operatorname{argmax}} \tilde{Q}(s_{j+1}, a, \xi; \mu_{\text{now}}, \sigma_{\text{now}})\).
- 用标准正态分布生成\(\xi'\)。用目标网络计算价值:
\(\widehat{q}_{j+1}^- = \tilde{Q}(s_{j+1}, \tilde{a}_{j+1}, \xi'; \mu_{\text{now}}^-, \sigma_{\text{now}}^-)\).
- 计算 TD 目标和 TD 误差:
\(\widehat{y}_j^- = r_j + \gamma \cdot \widehat{q}_{j+1}^-\)和\(\delta_j = \widehat{q}_j - \widehat{y}_j^-\).
- 设\(\alpha_\mu\)和\(\alpha_\sigma\)为学习率。做梯度下降更新噪声 DQN 的参数:
\(\begin{align*} \mu_{\text{new}} &\leftarrow \mu_{\text{now}} - \alpha_\mu \cdot \delta_j \cdot \nabla_\mu \widetilde{Q}(s_j, a_j, \xi; \mu_{\text{now}}, \sigma_{\text{now}}), \\ \sigma_{\text{new}} &\leftarrow \sigma_{\text{now}} - \alpha_\sigma \cdot \delta_j \cdot \nabla_\sigma \widetilde{Q}(s_j, a_j, \xi; \mu_{\text{now}}, \sigma_{\text{now}}). \end{align*}\).
- 设\(\tau \in (0, 1)\)是需要手动调整的超参数。做加权平均更新目标网络的参数:
\(\begin{align*} \mu_{\text{new}}^{-} &\leftarrow \tau \cdot \mu_{\text{new}} + (1 - \tau) \cdot \mu_{\text{now}}^{-}, \\ \sigma_{\text{new}}^{-} &\leftarrow \tau \cdot \sigma_{\text{new}} + (1 - \tau) \cdot \sigma_{\text{now}}^{-}. \end{align*}\).
总结
- 经验回放可以用于异策略算法。经验回放有两个好处:打破相邻两条经验的相关性、 重复利用收集的经验。
- 优先经验回放是对经验回放的一种改进。在做经验回放的时候,从经验回放数组中做加权随机抽样,TD 误差的绝对值大的经验被赋予较大的抽样概率、较小的学习率。
- Q 学习算法会造成 DQN 高估真实的价值。高估的原因有两个:第一,最大化造成TD 目标高估真实价值;第二,自举导致高估传播。高估并不是由 DQN 本身的缺陷造成的,而是由于 Q学习算法不够好。双 Q学习是对 Q 学习算法的改进,可以有效缓解高估。
- 对决网络与 DQN 一样,都是对最优动作价值函数\(Q^*\)的近似;两者的唯一区别在于神经网络结构。对决网络由两部分组成:\(D(s, a; w^D)\)是对最优优势函数的近似,\(V(s; w^V)\)是对最优状态价值函数的近似。对决网络的训练与 DQN 完全相同。
- 噪声网络是一种特殊的神经网络结构,神经网络中的参数带有随机噪声。噪声网络可以用于 DQN 等多种深度强化学习模型。噪声网络中的噪声可以鼓励探索,让智能体尝试不同的动作,这有利于学到更好的策略。