6.1 带基线的策略梯度方法

带基线的策略梯度方法

上一章推导出策略梯度，并介绍了两种策略梯度方法——REINFORCE 和 actor-critic。

虽然上一章的方法在理论上是正确的，但是在实践中效果并不理想。本章介绍的带基线的策略梯度 (policy gradient with baseline) 可以大幅提升策略梯度方法的表现。使用基线(baseline) 之后，REINFORCE 变成 REINFORCE with baseline, actor-critic 变成 advantage actor-critic (A2C)。

策略梯度中的基线

首先回顾上一章的内容。策略学习通过最大化目标函数\(J(\theta) = \mathbb{E}_S[V_\pi(S)]\)训练出策略网络\(\pi(a|s;\theta)\)。可以用策略梯度\(\nabla_\theta J(\theta)\)来更新参数\(\theta\)

\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} + \beta \cdot \nabla_\theta J(\theta_{\text{now}}).\)

策略梯度定理证明：

\(\nabla_\theta J(\theta) = \mathbb{E}_S\left[\mathbb{E}_{A\sim\pi(\cdot|S,\theta)}\left[Q_\pi(S,A) \cdot \nabla_\theta \ln \pi(A|S;\theta)\right]\right].\)

上一章中，我们对策略梯度\(\nabla_\theta J(\theta)\)做近似，推导出 REINFORCE 和 actor-critic; 两种方法区别在于具体如何做近似。

基线 (Baseline)

基于策略梯度公式 (8.1) 得出的 REINFORCE 和 actor-critic 方法效果通常不好。只需对策略梯度公式 (8.1) 做一个微小的改动，就能大幅提升表现：把\(b\)作为动作价值函数\(Q_\pi(S,A)\)的基线 (baseline), 用\(Q_\pi(S,A) - b\)

替换掉\(Q_\pi\)。设\(b\)是任意的函数，只要不依赖于动作\(A\)就可以，例如\(b\)可以是状态价值函数\(V_\pi(S)\)。

定理 8.1. 带基线的策略梯度定理

设\(b\)是任意的函数，但是\(b\)不能依赖于\(A\)。把\(b\)作为动作价值函数\(Q_\pi(S,A)\)的基线，对策略梯度没有影响：

\(\nabla_\theta J(\theta) = \mathbb{E}_S\left[\mathbb{E}_{A\sim\pi(\cdot|S;\theta)}\left[(Q_\pi(S,A) - b) \cdot \nabla_\theta \ln \pi(A|S;\theta)\right]\right].\)

定理 8.1 说明\(b\)的取值不影响策略梯度的正确性。不论是让\(b = 0\)还是让\(b = V_\pi(S)\), 对期望的结果毫无影响，期望的结果都会等于\(\nabla_\theta J(\theta)\)。其原因在于

\(\mathbb{E}_S\left[\mathbb{E}_{A\sim\pi(\cdot|S;\theta)}\left[b \cdot \nabla_\theta \ln \pi(A|S;\theta)\right]\right] = 0.\)

定理中的策略梯度表示成了期望的形式，我们对期望做蒙特卡洛近似。从环境中观测到一个状态\(s\),然后根据策略网络抽样得到\(a \sim \pi(\cdot|s;\theta)\)。那么策略梯度\(\nabla_\theta J(\theta)\)可以近似为下面的随机梯度：

\(\boldsymbol{g}_b(s,a;\theta) = \left[Q_\pi(s,a) - b\right] \cdot \nabla_\theta \ln \pi(a|s;\theta).\)

不论\(b\)的取值是 0 还是\(V_\pi(s)\), 得到的随机梯度\(\boldsymbol{g}_b(s,a;\theta)\)都是\(\nabla_\theta J(\theta)\)的无偏估计：

\(\text{Bias} = \mathbb{E}_{S,A}\left[\boldsymbol{g}_b(S,A;\theta)\right] - \nabla_\theta J(\theta) = 0.\)

虽然\(b\)的取值对\(\mathbb{E}_{S,A}\left[\boldsymbol{g}_b(S,A;\theta)\right]\)毫无影响，但是\(b\)对随机梯度\(\boldsymbol{g}_b(s,a;\theta)\)是有影响的。用不同的\(b\)

, 得到的方差

\(\text{Var} = \mathbb{E}_{S,A}\left\|\boldsymbol{g}_b(S,A;\theta) - \nabla_\theta J(\theta)\right\|^2\)

会有所不同。如果\(b\)很接近\(Q_\pi(s,a)\)关于\(a\)的均值，那么方差会比较小。因此，\(b = V_\pi(S)\)是很好的基线。

基线的直观解释

策略梯度公式期望中的\(Q_\pi(S,A) \cdot \nabla_\theta \ln \pi(A|S;\theta)\)的意义是什么呢？以图 8.1中的左图为例。

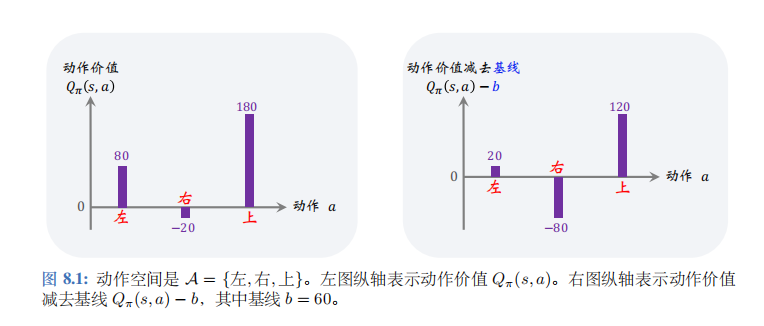
给定状态\(s_t\), 动作空间是\(A=\{左，右，上\}\), 动作价值函数给每个动作打分：

\(Q_\pi(s_t,左)=80, Q_\pi(s_t,右)=-20, Q_\pi(s_t,上)=180\)

这些分值会乘到梯度\(\nabla_\theta \ln \pi(A|S;\theta)\)上。在做完梯度上升之后，新的策略会倾向于分值高的动作。

• 动作价值\(Q_\pi(s_t,上)=180\)很大，说明基于状态\(s_t\)选择动作“上”是很好的决策。让梯度\(\nabla_\theta \ln \pi(上|s_t;\theta)\)乘以大的系数\(Q_\pi(s_t,上)=180\), 那么做梯度上升更新\(\theta\)之后，会让\(\pi(上|s_t;\theta)\)变大，在状态\(s_t\)的情况下更倾向于动作“上”。
• 相反，\(Q_\pi(s_t,右)=-20\)说明基于状态\(s_t\)选择动作“右”是糟糕的决策。让梯度\(\nabla_\theta \ln \pi(右|s_t;\theta)\)乘以负的系数\(Q_\pi(s_t,右)=-20\),那么做梯度上升更新\(\theta\)之后， 会让\(\pi(右|s_t;\theta)\)变小，在状态\(s_t\)的情况下选择动作“右”的概率更小。

根据上述分析，我们在乎的是动作价值\(Q_\pi(s_t,左)\)、\(Q_\pi(s_t,右)\)、\(Q_\pi(s_t,上)\)三者的相对大小，而非绝对大小。如果给三者都减去\(b=60\),那么三者的相对大小是不变的；动作“上”仍然是最好的，动作“右”仍然是最差的。因此\([Q_\pi(s_t,a_t) - b] \cdot \nabla_\theta \ln \pi(A|S;\theta)\)依然能指导\(\theta\)做调整，使得\(\pi(上|s_t;\theta)\)变大，而\(\pi(右|s_t;\theta)\)变小。