6.2 带基线的 REINFORCE 算法
带基线的 REINFORCE 算法
上一节推导出了带基线的策略梯度,并且对策略梯度做了蒙特卡洛近似。本节中,我们使用状态价值\(V_\pi(s)\)作基线,得到策略梯度的一个无偏估计:
\(\boldsymbol{g}(s,a;\theta) = \left[Q_\pi(s,a) - V_\pi(s)\right] \cdot \nabla_\theta \ln \pi(a|s;\theta).\)
我们在 深度强化学习(王树森)笔记03: 主要介绍policy network, policy gradient,REINFORCE 中学过 REINFORCE, 它使用实际观测的回报\(u\)来代替动作价值\(Q_\pi(S,A)\)。 此处我们同样用\(u\)代替\(Q_\pi(S,A)\)。此外,我们还用一个神经网络\(v(s;w)\)近似状态价值函数\(V_\pi(S)\)。这样一来,\(\boldsymbol{g}(s,a;\theta)\)就被近似成了:
\(\tilde{\boldsymbol{g}}(s,a;\theta) = \left[u - v(s;w)\right] \cdot \nabla_\theta \ln \pi(a|s;\theta).\)
可以用\(\tilde{\boldsymbol{g}}(s,a;\theta)\)作为策略梯度\(\nabla_\theta J(\theta)\)的近似,更新策略网络参数:
\(\theta \leftarrow \theta + \beta \cdot \tilde{\boldsymbol{g}}(s,a;\theta).\)
策略网络和价值网络
带基线的 REINFORCE 需要两个神经网络:策略网络\(\pi(a|s;\theta)\)和价值网络\(v(s;w)\);
神经网络结构如图 8.2 和 8.3 所示。策略网络与之前章节一样:输入是状态\(s\), 输出是一个向量,每个元素表示一个动作的概率。
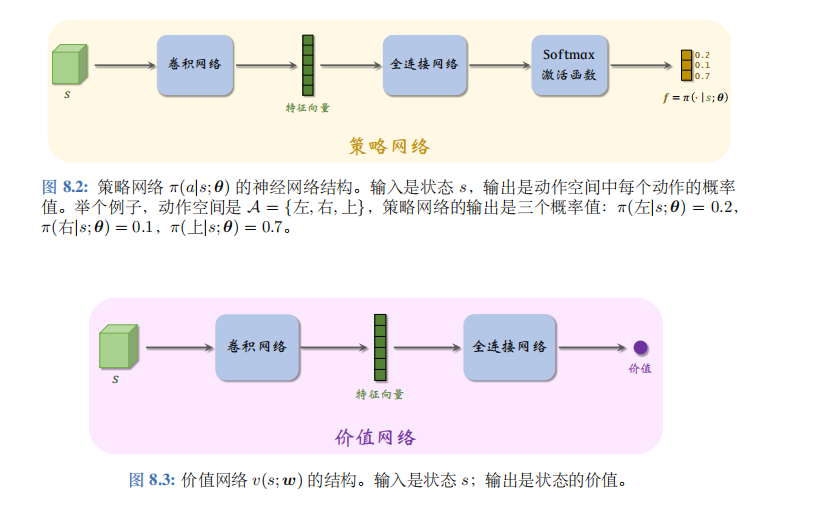
此处的价值网络\(v(s;w)\)与之前使用的价值网络\(q(s,a;w)\)区别较大。此处的\(v(s;w)\)是对状态价值\(V_\pi\)的近似,而非对动作价值\(Q_\pi\)的近似。\(v(s;w)\)的输入是状态\(s\), 输出是一个实数,作为基线。策略网络和价值网络的输入都是状态\(s\),因此可以让两个神经网络共享卷积网络的参数,这是编程实现中常用的技巧。
虽然带基线的 REINFORCE 有一个策略网络和一个价值网络,但是这种方法不是actor-critic。价值网络没有起到“评委”的作用,只是作为基线而已,目的在于降低方差,加速收敛。真正帮助策略网络(演员)改进参数\(\theta\)的不是价值网络,而是实际观测到的回报\(u\)。

算法的推导
训练策略网络 的方法是近似的策略梯度上升。从\(t\)时刻开始, 智能体完成一局游戏,观测到全部奖励\(r_t, r_{t+1}, \cdots, r_n\)然后计算回报\(u_t = \sum_{k=t}^n \gamma^{k-t} \cdot r_k\)。让价值网络做出预测\(\hat{v}_t = v(s_t;w)\),作为基线。这样就得到了带基线的策略梯度:
\(\tilde{\boldsymbol{g}}(s_t,a_t;\theta) = (u_t - \hat{v}_t) \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta).\)
它是策略梯度\(\nabla_\theta J(\theta)\)的近似。最后做梯度上升更新\(\theta\):
\(\theta \leftarrow \theta + \beta \cdot \tilde{\boldsymbol{g}}(s_t,a_t;\theta).\)
这样可以让目标函数\(J(\theta)\)逐渐增大。
训练价值网络 的方法是回归 (regression)。回忆一下,状态价值是回报的期望:
\(V_\pi(s_t) = \mathbb{E}[U_t | S_t = s_t],\)
期望消掉了动作\(A_t, A_{t+1}, \cdots, A_n\)和状态\(S_{t+1}, \cdots, S_n\)。训练价值网络的目的是让\(v(s_t;w)\)拟合\(V_\pi(s_t)\)
,即拟合\(u_t\)的期望。定义损失函数:
\(L(w) = \frac{1}{2n} \sum_{t=1}^{n} [v(s_t;w) - u_t]^2.\)
设\(\hat{v}_t = v(s_t;w)\)。损失函数的梯度是:
\(\nabla_w L(w) = \frac{1}{n} \sum_{t=1}^{n} (\hat{v}_t - u_t) \cdot \nabla_w v(s_t;w).\)
做一次梯度下降更新\(w\):
\(w \leftarrow w - \alpha \cdot \nabla_w L(w).\)
训练流程
当前策略网络的参数是\(\theta_{\text{now}}\),价值网络的参数是\(w_{\text{now}}\)。执行下面的步骤,对参数做一轮更新。
- 用策略网络\(\theta_{\text{now}}\)控制智能体从头开始玩一局游戏,得到一条轨迹 (trajectory):
\(s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_n, a_n, r_n.\)
- 计算所有的回报:
\(u_t = \sum_{k=t}^n \gamma^{k-t} \cdot r_k, \quad \forall t = 1, \cdots, n.\)
- 让价值网络做预测:
\(\hat{v}_t = v(s_t; w_{\text{now}}), \quad \forall t = 1, \cdots, n.\)
- 计算误差
\(\delta_t = \hat{v}_t - u_t, \quad \forall t = 1, \cdots, n.\)
- 用\(\{s_t\}_{t=1}^n\)作为价值网络输入,做反向传播计算:
\(\nabla_w v(s_t; w_{\text{now}}), \quad \forall t = 1, \cdots, n.\)
- 更新价值网络参数:
\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \sum_{t=1}^{n} \delta_t \cdot \nabla_w v(s_t; w_{\text{now}}).\)
- 用\(\{(s_t, a_t)\}_{t=1}^n\)作为数据,做反向传播计算:
\(\nabla_\theta \ln \pi(a_t | s_t; \theta_{\text{now}}), \quad \forall t = 1, \cdots, n.\)
- 做随机梯度上升更新策略网络参数:
\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} - \beta \cdot \sum_{t=1}^{n} \gamma^{t-1} \cdot \delta_t \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta_{\text{now}}).\)