6.3 Advantage Actor-Critic (A2C)
Advantage Actor-Critic (A2C)
之前我们推导出了带基线的策略梯度,并且对策略梯度做了蒙特卡洛近似,得到策略梯度的一个无偏估计:
\(g(s, a; \theta) = \left[ Q_\pi(s, a) - V_\pi(s) \right] \cdot \nabla_\theta \ln \pi(a | s; \theta). \quad (8.2)\)
公式中的\(Q_\pi - V_\pi\)被称作优势函数 (advantage function)。因此,基于上面公式得到的actor-critic 方法被称为 advantage actor-critic, 缩写 A2C。
A2C 属于 actor-critic 方法。有一个策略网络\(\pi(a|s;\theta)\),相当于演员,用于控制智能体运动。还有一个价值网络\(v(s;w)\),相当于评委,他的评分可以帮助策略网络 (演员) 改进技术。两个神经网络的结构与上一节中的完全相同,但是本节和上一节用不同的方法训练两个神经网络。
算法推导
训练价值网络:训练价值网络\(v(s;w)\)的算法是从贝尔曼公式来的:
\(V_\pi(s_t) = \mathbb{E}_{A_t \sim \pi(\cdot|s_t;\theta)}\left[ \mathbb{E}_{S_{t+1} \sim p(\cdot|s_t,A_t)}\left[R_t + \gamma \cdot V_\pi(S_{t+1})\right] \right].\)
我们对贝尔曼方程左右两边做近似:
- 方程左边的\(V_\pi(s_t)\)可以近似成\(v(s_t;w)\)。\(v(s_t;w)\)是价值网络在\(t\)时刻对\(V_\pi(s_t)\)做出的估计。
- 方程右边的期望是关于当前时刻动作\(A_t\)与下一时刻状态\(S_{t+1}\)求的。给定当前状态\(s_t\),智能体执行动作\(a_t\),环境会给出奖励\(r_t\)和新的状态\(s_{t+1}\)。用观测到的\(r_t\)、\(s_{t+1}\)对期望做蒙特卡洛近似,得到:
\(r_t + \gamma \cdot V_\pi(s_{t+1}).\)
- 进一步把公式中的\(V_\pi(s_{t+1})\)近似成\(v(s_{t+1};w)\), 得到
\(\hat{y}_t \triangleq r_t + \gamma \cdot v(s_{t+1};w).\)
把它称作 TD 目标。它是价值网络在\(t+1\)时刻对\(V_\pi(s_t)\)做出的估计。\(v(s_t;w)\)和\(\hat{y}_t\)都是对动作价值\(V_\pi(s_t)\)的估计。由于\(\hat{y}_t\)部分基于真实观测到的奖励\(r_t\),我们认为\(\hat{y}_t\)比\(v(s_t;w)\)更可靠。所以把\(\hat{y}_t\)固定住,更新\(w\), 使得\(v(s_t;w)\)更接近\(\hat{y}_t\)。
具体这样更新价值网络参数\(w\)。定义损失函数
\(L(w) \triangleq \frac{1}{2} [v(s_t;w) - \hat{y}_t]^2.\)
设\(\hat{v}_t \triangleq v(s_t;w)\)。损失函数的梯度是:
\(\nabla_w L(w) = (\hat{v}_t - \hat{y}_t) \cdot \nabla_w v(s_t;w).\)
定义 TD 误差为
\(\delta_t \triangleq \hat{v}_t - \hat{y}_t.\)
做一轮梯度下降更新\(w\):
\(w \leftarrow w - \alpha \cdot \delta_t \cdot \nabla_w v(s_t;w).\)
这样可以让价值网络的预测\(v(s_t;w)\)更接近\(\hat{y}_t\)。
训练策略网络:A2C 从公式出发,对\(\boldsymbol{g}(s,a;\theta)\)做近似,记作\(\tilde{\boldsymbol{g}}\), 然后用\(\tilde{\boldsymbol{g}}\)更新策略网络参数\(\theta\)。下面我们做数学推导。回忆一下贝尔曼公式:
\(Q_\pi(s_t,a_t) = \mathbb{E}_{S_{t+1} \sim p(\cdot|s_t,a_t)}\left[R_t + \gamma \cdot V_\pi(S_{t+1})\right].\)
把近似策略梯度\(\boldsymbol{g}(s_t,u_t;\theta)\)中的\(Q_\pi(s_t,a_t)\)替换成上面的期望,得到:
\(\begin{align*} g(s_t, a_t; \theta) &= \left[Q_{\pi}(s_t, a_t) - V_{\pi}(s_t)\right] \cdot \nabla_{\theta} \ln \pi(a_t \mid s_t; \theta) \\ &= \left[E_{S_{t+1}}\left[R_t + \gamma \cdot V_{\pi}(S_{t+1})\right] - V_{\pi}(s_t)\right] \cdot \nabla_{\theta} \ln \pi(a_t \mid s_t; \theta). \end{align*}\)
当智能体执行动作\(a_t\)之后,环境给出新的状态\(s_{t+1}\)和奖励\(r_t\); 利用\(s_{t+1}\)和\(r_t\)对上面的期望做蒙特卡洛近似,得到:
\(\boldsymbol{g}(s_t,a_t;\theta) \approx [r_t + \gamma \cdot V_\pi(s_{t+1}) - V_\pi(s_t)] \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta).\)
进一步把状态价值函数\(V_\pi(s)\)替换成价值网络\(v(s;w)\), 得到:
\(\tilde{\boldsymbol{g}}(s_t,a_t;\theta) \triangleq [r_t + \gamma \cdot v(s_{t+1};w) - v(s_t;w)] \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta).\)
前面定义了 TD 目标和 TD 误差:
\(\hat{y}_t \triangleq r_t + \gamma \cdot v(s_{t+1};w)\)和\(\delta_t \triangleq \hat{v}_t - \hat{y}_t.\)
因此,可以把\(\tilde{\boldsymbol{g}}(s_t,a_t;\theta)\)写成:
\(\tilde{\boldsymbol{g}}(s_t,a_t;\theta) \triangleq -\delta_t \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta).\)
\(\tilde{\boldsymbol{g}}\)是\(\boldsymbol{g}\)的近似,所以也是策略梯度\(\nabla_\theta J(\theta)\)的近似。用\(\tilde{\boldsymbol{g}}\)更新策略网络参数\(\theta\):
\(\theta \leftarrow \theta + \beta \cdot \tilde{\boldsymbol{g}}(s_t,a_t;\theta).\)
这样可以让目标函数\(J(\theta)\)变大。
策略网络与价值网络的关系 : A2C 中策略网络 (演员) 和价值网络 (评委) 的关系如图 8.4 所示。
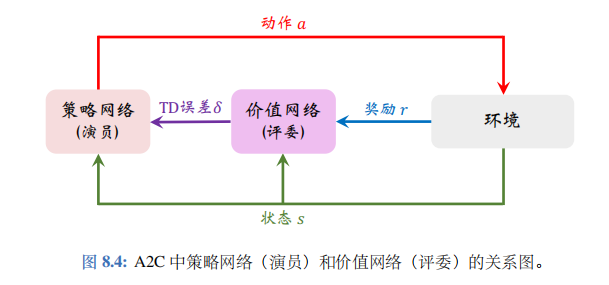
智能体由策略网络 π 控制,与环境交互,并收集状态、动作、奖励。策略网络(演员) 基于状态\(s_t\)做出动作\(a_t\)。价值网络 (评委) 基于\(s_t\)、\(s_{t+1}\)、\(r_t\)算出 TD 误差\(\delta_t\)。策略网络(演员) 依靠\(\delta_t\)来判断自己动作的好坏,从而改进自己的演技 (即参数\(\theta\))。
读者可能会有疑问: 价值网络\(v\)只知道两个状态\(s_t\)、\(s_{t+1}\),而并不知道动作\(a_t\),那么价值网络为什么能评价\(a_t\)的好坏呢?价值网络\(v\)告诉策略网络\(\pi\)的唯一信息是\(\delta_t\)。回顾一下\(\delta_t\)的定义:
\(-\delta_t = \underbrace{r_t + \gamma \cdot v(s_{t+1}; \boldsymbol{w})}_{\text{TD目标} \hat{y}_t} - \underbrace{v(s_t; \boldsymbol{w})}_{\text{基线}}.\)
基线\(v(s_t;w)\)是价值网络在\(t\)时刻对\(\mathbb{E}[U_t]\)的估计;此时智能体尚未执行动作\(a_t\)。而 TD 目标\(\hat{y}_t\)是价值网络在\(t+1\)时刻对\(\mathbb{E}[U_t]\)的估计;此时智能体已经执行动作\(a_t\)。
- 如果\(\hat{y}_t > v(s_t;w)\),说明动作\(a_t\)很好,使得奖励\(r_t\)超出预期,或者新的状态\(s_{t+1}\)比预期好;这种情况下应该更新\(\theta\),使得\(\pi(a_t | s_t;\theta)\)变大。
- 如果\(\hat{y}_t < v(s_t;w)\),说明动作\(a_t\)不好,导致奖励\(r_t\)不及预期,或者新的状态\(s_{t+1}\)比预期差;这种情况下应该更新\(\theta\),使得\(\pi(a_t | s_t;\theta)\)减小。
综上所述,\(\delta_t\)中虽然不包含动作\(a_t\),但是\(\delta_t\)可以间接反映出动作\(a_t\)的好坏,可以帮助策略网络(演员) 改进演技。
训练流程下面概括 A2C 训练流程。设当前策略网络参数是\(\theta_{\text{now}}\),价值网络参数是\(w_{\text{now}}\)。执行下面的步骤,将参数更新成\(\theta_{\text{new}}\)和\(w_{\text{new}}\):
- 观测到当前状态\(s_t\),根据策略网络做决策\(a_t \sim \pi(\cdot|s_t;\theta_{\text{now}})\),并让智能体执行动作\(a_t\)。
- 从环境中观测到奖励\(r_t\)和新的状态\(s_{t+1}\)。
- 让价值网络打分:\(\hat{v}_t = v(s_t; w_{\text{now}})\)和\(\hat{v}_{t+1} = v(s_{t+1}; w_{\text{now}})\)。
- 计算 TD 目标和 TD 误差:\(\hat{y}_t = r_t + \gamma \cdot \hat{v}_{t+1}\)和\(\delta_t = \hat{v}_t - \hat{y}_t\)。
- 更新价值网络:
\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \delta_t \cdot \nabla_w v(s_t; w_{\text{now}}).\)
- 更新策略网络:
\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} - \beta \cdot \delta_t \cdot \nabla_\theta \ln \pi(a_t | s_t; \theta_{\text{now}}).\)
注 此处训练策略网络和价值网络的方法属于同策略(on-policy),要求行为策略(behavion policy)与目标策略 (target policy) 相同,都是最新的策略网络\(\pi(a|s;\theta_{\text{now}})\)。不能使用经验回放,因为经验回放数组中的数据是用旧的策略网络\(\pi(a|s;\theta_{\text{old}})\)获取的,不能在当前重复利用。
用目标网络改进训练
上述训练价值网络的算法存在自举——即用价值网络自己的估值\(\hat{v}_{t+1}\)去更新价值网络自己。为了缓解自举造成的偏差,可以使用目标网络(target network) 计算 TD 目标。把目标网络记作\(v(s;w^-)\), 它的结构与价值网络的结构相同,但是参数不同。使用目标网络计算 TD 目标,那么 A2C 的训练就变成了:
- 观测到当前状态\(s_t\),根据策略网络做决策\(a_t \sim \pi(\cdot|s_t;\theta_{\text{now}})\), 并让智能体执行动作\(a_t\)。
- 从环境中观测到奖励\(r_t\)和新的状态\(s_{t+1}\)。
- 让价值网络给\(s_t\)打分:\(\hat{v}_t = v(s_t; w_{\text{now}})\)。
- 让目标网络给\(s_{t+1}\)打分:\(\hat{v}_{t+1}^- = v(s_{t+1}; w_{\text{now}}^-)\)。
- 计算 TD 目标和 TD 误差:\(\hat{y}_t^- = r_t + \gamma \cdot \hat{v}_{t+1}^-\)和\(\delta_t = \hat{v}_t - \hat{y}_t^-\)。
- 更新价值网络:
\(w_{\text{new}} \leftarrow w_{\text{now}} - \alpha \cdot \delta_t \cdot \nabla_w v(s_t; w_{\text{now}}).\)
- 更新策略网络:
\(\theta_{\text{new}} \leftarrow \theta_{\text{now}} - \beta \cdot \delta_t \cdot \nabla\theta \ln \pi(a_t | s_t; \theta{\text{now}}).\)
- 设\(\tau \in (0,1)\)是需要手动调的超参数。做加权平均更新目标网络的参数:
\(\bar{w}_{\text{new}} \leftarrow \tau \cdot w_{\text{new}} + (1-\tau) \cdot w_{\text{now}}^-.\)
总结
- 在策略梯度中加入基线 (baseline) 可以降低方差,显著提升实验效果。实践中常用\(b = V_\pi(s)\)作为基线。
- 可以用基线来改进 REINFORCE 算法。价值网络\(v(s;w)\)近似状态价值函数\(V_\pi(s)\),把\(v(s;w)\)作为基线。用策略梯度上升来更新策略网络\(\pi(a|s;\theta)\)。用蒙特卡洛(而非自举) 来更新价值网络\(v(s;w)\)。
- 可以用基线来改进 actor-critic, 得到的方法叫做 advantage actor-critic(A2C),它也有一个策略网络\(\pi(a|s;\theta)\)和一个价值网络\(v(s;\theta)\)。用策略梯度上升来更新策略网络,用 TD 算法来更新价值网络。
- 多步TD target

- a2c vs REINFORCE
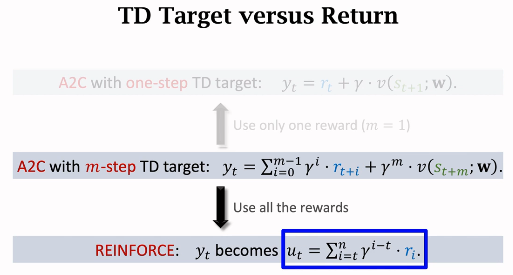

reinforce是a2c的特例 , a2c是reinforce的特例