7.1 连续控制

连续控制

前面的内容全部都是离散控制，即动作空间是一个离散的集合，比如超级玛丽游戏中的动作空间\(A=\{左，右，上\}\)是个离散集合。本章的内容是连续控制，即动作空间是个连续集合，比如汽车的转向\(A=[-40^{\circ},40^{\circ}]\)就是连续集合。如果把连续动作空间做离散化，那么离散控制的方法就能直接解决连续控制问题；先讨论连续集合的离散化。然而更好的办法是直接用连续控制方法，而非离散化之后借用离散控制方法。本章介绍两种连续控制方法：确定策略网络和随机策略网络。

ChatGPT对DPG的解释：

确定性策略梯度（Deterministic Policy Gradient，DPG）是强化学习中一种用于训练确定性策略的方法。与传统的随机策略不同，确定性策略直接映射状态到具体的动作，而不是输出一个动作的概率分布。DPG 主要应用于连续动作空间的问题，其中动作是实数空间中的连续值。

下面是 DPG 的基本思想和主要要素：

1. 确定性策略： 在 DPG 中，智能体的策略是确定性的，即给定一个状态，它直接输出一个具体的动作。这样的确定性策略可以表示为 (\(a = \mu(s)\))，其中 (\(\mu\)) 是策略函数，输入为状态 (s)，输出为动作 (a)。
2. 值函数： DPG 使用值函数来评估策略的好坏。通常，包括状态值函数（State Value Function）和动作值函数（Action Value Function）。其中，状态值函数表示在给定状态下的期望累积回报，动作值函数表示在给定状态和动作的情况下的期望累积回报。
3. 策略梯度： DPG 使用策略梯度方法来更新策略参数。策略梯度是关于策略参数的梯度，它告诉我们如何调整策略以最大化期望累积回报。在 DPG 中，通过对值函数对动作的梯度来计算策略梯度。
4. Actor-Critic 结构： DPG 通常采用 Actor-Critic 结构，其中包括一个 Actor 网络负责输出动作，一个 Critic 网络负责估计值函数。这两个网络共同工作，Actor 的参数通过 Critic 的估计值函数的梯度进行更新。

总体来说，DPG 的训练过程涉及通过策略梯度来调整 Actor 网络的参数，以最大化 Critic 网络估计的值函数。这样，DPG 可以在连续动作空间中有效地训练确定性策略。

离散控制与连续控制的区别

考虑这样一个问题：我们需要控制一只机械手臂，完成某些任务，获取奖励。机械手臂有两个关节，分别可以在\([0^{\circ},360^{\circ}]\)与\([0^{\circ},180^{\circ}]\)的范围内转动。这个问题的自由度是\(d=2\), 动作是二维向量，动作空间是连续集合\(A=[0,360] \times [0,180]\)。

此前我们学过的强化学习方法全部都是针对离散动作空间，不能直接解决上述连续控制问题。想把此前学过的离散控制方法应用到连续控制上，必须要对连续动作空间做离散化 (网格化)。比如把连续集合\(A=[0,360] \times [0,180]\)变成离散集合\(\{0,20,40,\cdots,360\} \times \{0,20,40,\cdots,180\}\); 见图 10.1。

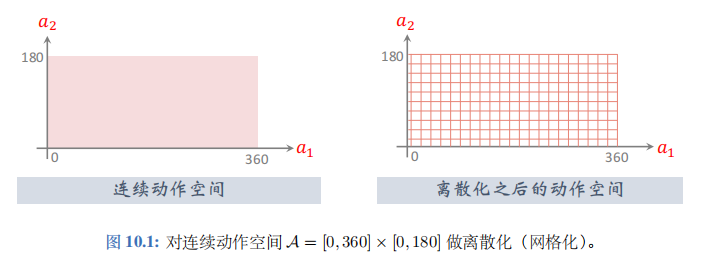
对动作空间做离散化之后，就可以应用之前学过的方法训练 DQN 或者策略网络，用于控制机械手臂。可是用离散化解决连续控制问题有个缺点。把自由度记作\(d\)。自由度\(d\)越大，网格上的点就越多，而且数量随着\(d\)指数增长，会造成维度灾难。动作空间的大小即网格上点的数量。如果动作空间太大，DQN 和策略网络的训练都变得很困难，强化学习的结果会不好。上述离散化方法只适用于自由度\(d\)很小的情况；如果\(d\)不是很小，就应该使用连续控制方法。后面两节介绍两种连续控制的方法。