7.2 确定策略梯度 (DPG)
确定策略梯度 (DPG)
确定策略梯度 (deterministic policy gradient, DPG) 是最常用的连续控制方法。DPG 是一种 actor-critic 方法,它有一个策略网络 (演员), 一个价值网络 (评委)。策略网络控制智能体做运动,它基于状态\(s\)做出动作\(a\)。价值网络不控制智能体,只是基于状态\(s\)给动作\(a\)打分,从而指导策略网络做出改进。图 10.2 是两个神经网络的关系。
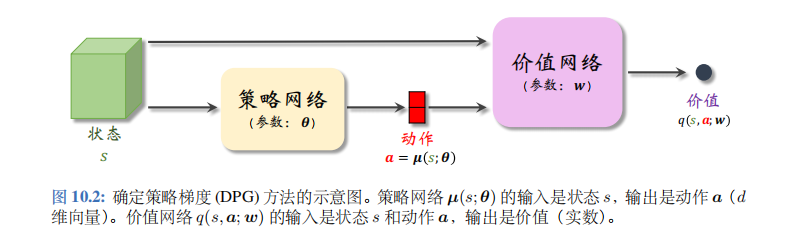
策略网络和价值网络
本节的策略网络不同于前面章节的策略网络。在之前章节里,策略网络\(\pi(a|s;\theta)\)是一个概率质量函数,它输出的是概率值。本节的确定策略网络\(\mu(s;\theta)\)的输出是\(d\)维的向量\(a\),作为动作。两种策略网络一个是随机的,一个是确定性的:
- 之前章节中的策略网络\(\pi(a|s;\theta)\)带有随机性:给定状态\(s\), 策略网络输出的是离散动作空间\(A\)上的概率分布;
- 本节的确定策略网络没有随机性:对于确定的状态\(s\), 策略网络\(\mu\)输出的动作\(a\)是确定的。动作\(a\)直接是\(\mu\)的输出,而非随机抽样得到的。
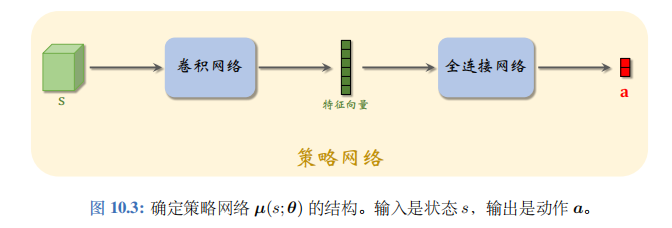
确定策略网络\(\mu\)的结构如图 10.3 所示。如果输入的状态\(s\)是个矩阵或者张量 (例如图片、视频),那么\(\mu\)就由若干卷积层、全连接层等组成。
确定策略可以看做是随机策略的一个特例。确定策略\(\mu(s;\theta)\)的输出是\(d\)维向量,它的第\(i\)个元素记作\(\hat{\mu}_i=[\mu(s;\theta)]_i\)。定义下面这个随机策略:
\(\pi(a|s;\theta,\sigma)=\prod_{i=1}^d\frac{1}{\sqrt{6.28}\sigma_i}\cdot\exp\left(-\frac{[a_i-\hat{\mu}_i]^2}{2\sigma_i^2}\right). \quad{(10.1)}\)
这个随机策略是均值为\(\mu(s;\theta)\)、协方差矩阵为\(\text{diag}(\sigma_1,\cdots,\sigma_d)\)的多元正态分布。本节的确定策略可以看做是上述随机策略在\(\sigma=[\sigma_1,\cdots,\sigma_d]\)为全零向量时的特例。
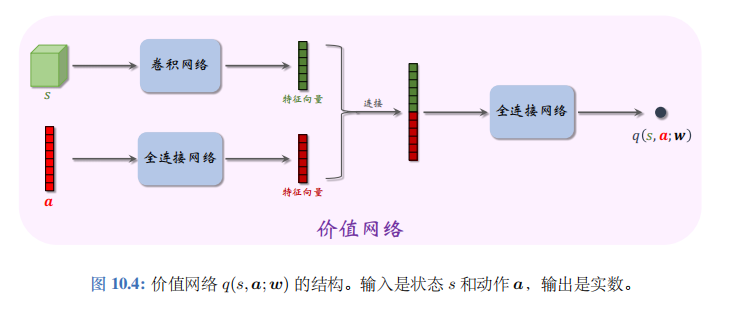
本节的价值网络\(q(s,a;w)\)是对动作价值函数\(Q_{\pi}(s,a)\)的近似。价值网络的结构如图 10.4 所示。价值网络的输入是状态\(s\)和动作\(a\),输出的价值\(\hat{q}=q(s,a;w)\)是个实数,可以反映动作的好坏;动作\(a\)越好,则价值\(\hat{q}\)就越大。所以价值网络可以评价策略网络的表现。在训练的过程中,价值网络帮助训练策略网络;在训练结束之后,价值网络就被丢弃,由策略网络控制智能体。
算法推导
用行为策略收集经验:
本节的确定策略网络属于异策略(off-policy) 方法,即行为策略 (behavior policy) 可以不同于目标策略 (target policy)。目标策略即确定策略网络\(\mu(s;\theta_{now})\),其中\(\theta_{now}\)是策略网络最新的参数。行为策略可以是任意的,比如
\(a=\mu(s;\theta_{old})+\epsilon\).
公式的意思是行为策略可以用过时的策略网络参数,而且可以往动作中加入噪声\(\epsilon \in \mathbb{R}^d\)。异策略的好处在于可以把收集经验与训练神经网络分割开;把收集到的经验存入经验回放数组(replay buffer),在做训练的时候重复利用收集到的经验。见图 10.5。
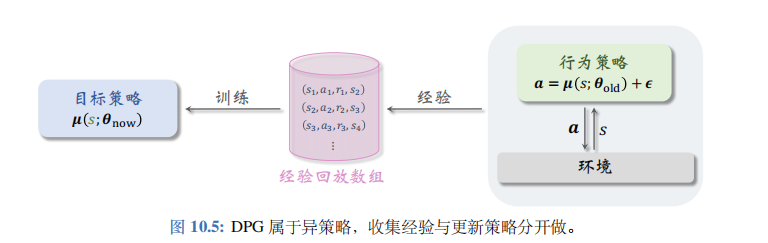
用行为策略控制智能体与环境交互,把智能体的轨迹(trajectory) 整理成\((s_t,a_t,r_t,s_{t+1})\)这样的四元组,存入经验回放数组。在训练的时候,随机从数组中抽取一个四元组,记作\((s_j,a_j,r_j,s_{j+1})\)。在训练策略网络\(\mu(s;\theta)\)的时候,只用到状态\(s_j\)。在训练价值网络\(q(s,a;w)\)的时候,要用到四元组中全部四个元素:\(s_j,a_j,r_j,s_{j+1}\)。
训练策略网络:
首先通俗解释训练策略网络的原理。如图 10.6 所示,给定状态\(s\),策略网络输出一个动作\(a=\mu(s;\theta)\),然后价值网络会给\(a\)打一个分数:\(\hat{q}=q(s,a;w)\)。
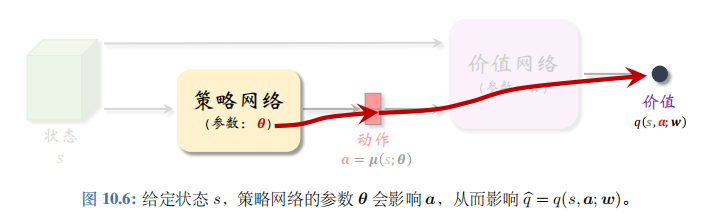
参数\(\theta\)影响\(a\), 从而影响\(\hat{q}\)。分数\(\hat{q}\)可以反映出\(\theta\)的好坏程度。训练策略网络的目标就是改进参数\(\theta\),使\(\hat{q}\)变得更大。把策略网络看做演员,价值网络看做评委。训练演员(策略网络)的目的就是让他迎合评委 (价值网络) 的喜好,改变自己的表演技巧 (即参数\(\theta\)), 使得评委打分\(\hat{q}\)的均值更高。
根据以上解释,我们来推导目标函数。如果当前状态是\(s\), 那么价值网络的打分就是:
\(q(s,\mu(s;\theta);w)\)。
我们希望打分的期望尽量高,所以把目标函数定义为打分的期望:
\(J(\theta)=\mathbb{E}_S[q(S,\mu(S;\theta);w)]\)。
关于状态\(S\)求期望消除掉了\(S\)的影响;不管面对什么样的状态\(S\), 策略网络(演员)都应该做出很好的动作,使得平均分\(J(\theta)\)尽量高。策略网络的学习可以建模成这样一个最大化问题:
\(\max_{\theta}J(\theta)\)。
注意,这里我们只训练策略网络,所以最大化问题中的优化变量是策略网络的参数\(\theta\),而价值网络的参数\(w\)被固定住。
可以用梯度上升来增大\(J(\theta)\)。每次用随机变量\(S\)的一个观测值(记作\(s_j\)) 来计算梯度:\(g_j \triangleq \nabla_{\theta}q(s_j,\mu(s_j;\theta);w)\)。
它是\(\nabla_{\theta} J(\theta)\)的无偏估计。\(g_j\)叫做确定策略梯度 (deterministic policy gradient), 缩写DPG。
可以用链式法则求出梯度\(g_j\)。复习一下链式法则。如果有这样的函数关系\(\theta \to a \to q\),那么\(q\)关于\(\theta\)的导数可以写成
\(\frac{\partial q}{\partial \theta} = \frac{\partial a}{\partial \theta} \cdot \frac{\partial q}{\partial a}\)。
价值网络的输出与\(\theta\)的函数关系如图 10.6 所示。应用链式法则,我们得到下面的定理。
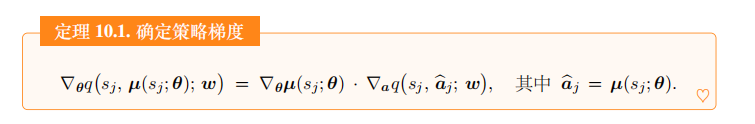
定理 10.1. 确定策略梯度
\(\nabla_{\theta}q(s_j,\mu(s_j;\theta);w)=\nabla_{\theta}\mu(s_j;\theta) \cdot \nabla_a q(s_j,\hat{a}_j;w), \quad \text{其中} \quad \hat{a}_j=\mu(s_j;\theta).\)
由此我们得到更新\(\theta\)的算法。每次从经验回放数组里随机抽取一个状态,记作\(s_j\)。计算\(\hat{a}_j=\mu(s_j;\theta)\)。用梯度上升更新一次\(\theta\):
\(\theta \leftarrow \theta + \beta \cdot \nabla_{\theta}\mu(s_j;\theta) \cdot \nabla_a q(s_j,\hat{a}_j;w).\)
此处的\(\beta\)是学习率,需要手动调。这样做梯度上升,可以逐渐让目标函数\(J(\theta)\)增大,也就是让评委给演员的平均打分更高。

解决办法:

训练价值网络:
首先通俗解释训练价值网络的原理。训练价值网络的目标是让价值网络\(q(s,a;w)\)的预测越来越接近真实价值函数\(Q_{\pi}(s,a)\)。如果把价值网络看做评委,那么训练评委的目标就是让他的打分越来越准确。每一轮训练都要用到一个实际观测的奖励\(r\),可以把\(r\)看做“真理”,用它来校准评委的打分。
训练价值网络要用 TD 算法。这里的 TD 算法与之前学过的标准 actor-critic 类似,都是让价值网络去拟合 TD 目标。每次从经验回放数组中取出一个四元组\((s_j,a_j,r_j,s_{j+1})\), 用它更新一次参数\(w\)。首先让价值网络做预测:
\(\hat{q}_j=q(s_j,a_j;w) \quad \text{和} \quad \hat{q}_{j+1}=q(s_{j+1},\mu(s_{j+1};\theta);w)\)
计算 TD 目标\(\hat{y}_j=r_j+\gamma \cdot \hat{g}_{j+1}\).定义损失函数
\(L(w)=\frac{1}{2}\left[q(s_j,a_j;w)-\hat{y}_j\right]^2,\)
计算梯度
\(\nabla_{w} L(w) = \underbrace{\left(\hat{q}_{j} - \hat{y}_{j}\right)}_{\text{TD误差} \delta_{j}} \cdot \nabla_{w} q\left(s_{j}, a_{j}; w\right),\)
做一轮梯度下降更新参数\(w\):
\(w \leftarrow w - \alpha \cdot \nabla_{w} L(w)\)
这样可以让损失函数\(L(w)\)减小,也就是让价值网络的预测\(\hat{q}_j=q(s,a;w)\)更接近 TD 目标\(\hat{y}_j\)。公式中的\(\alpha\)是学习率,需要手动调。
训练流程:
做训练的时候,可以同时对价值网络和策略网络做训练。每次从经验回放数组中抽取一个四元组,记作\((s_j,a_j,r_j,s_{j+1})\)。把神经网络当前参数记作\(w_{now}\)和\(\theta_{now}\)。执行以下步骤更新策略网络和价值网络:
- 让策略网络做预测:\(\hat{a}_j=\mu(s_j;\theta_{now})\)和\(\hat{a}_{j+1}=\mu(s_{j+1};\theta_{now})\).
- 让价值网络做预测:\(\hat{q}_j=q(s_j,a_j;w_{now})\)和\(\hat{q}_{j+1}=q(s_{j+1},\hat{a}_{j+1};w_{now})\).
- 计算 TD 目标和 TD 误差:\(\hat{y}_j=r_j+\gamma \cdot \hat{q}_{j+1}\)和\(\delta_j=\hat{q}_j-\hat{y}_j\).
- 更新价值网络:\(w_{new}=w_{now}-\alpha \cdot \delta_j \cdot \nabla_w q(s_j,a_j;w_{now})\).
- 更新策略网络:\(\theta_{new}=\theta_{now}+\beta \cdot \nabla_{\theta}\mu(s_j;\theta_{now}) \cdot \nabla_a q(s_j,\hat{a}j;w_{now})\).
在实践中,上述算法的表现并不好;读者应当采用后面介绍的技巧训练策略网络和价值网络。

深入分析 DPG
上一节介绍的 DPG 是一种“四不像”的方法。DPG 乍看起来很像前面介绍的策略学习方法,因为 DPG 的目的是学习一个策略\(\mu\),而价值网络\(q\)只起辅助作用。然而 DPG 又很像之前介绍的 DQN, 两者都是异策略 (Off-policy), 而且两者存在高估问题。鉴于 DPG 的重要性,我们更深入分析 DPG。
从策略学习的角度看待 DPG

答案是动作价值函数\(Q_{\pi}(s,a)\)。上一节 DPG 的训练流程中,更新价值网络用到 TD 目标:\(\hat{y}_j=r_j+\gamma \cdot q(s_{j+1},\mu(s_{j+1};\theta_{now});w_{now})\)。
很显然,当前的策略\(\mu(s;\theta_{now})\)会直接影响价值网络\(q\)。策略不同,得到的价值网络\(q\)就不同。
虽然价值网络\(q(s,a;w)\)通常是对动作价值函数\(Q_{\pi}(s,a)\)的近似,但是我们最终的目标是让\(q(s,a;w)\)趋近于最优动作价值函数\(Q^{\star}(s,a)\)。回忆一下,如果\(\pi\)是最优策略\(\pi^{\star}\), 那么\(Q_{\pi}(s,a)\)就等于\(Q^{\star}(s,a)\)。训练 DPG 的目的是让\(\mu(s;\theta)\)趋近于最优策略\(\pi^{\star}\)那么理想情况下,\(q(s,a;w)\)最终趋近于\(Q^{\star}(s,a)\)。

答案是目标策略\(\mu(s;\theta_{now})\),因为目标策略对价值网络的影响很大。在理想情况下,行为策略对价值网络没有影响。我们用 TD 算法训练价值网络,TD 算法的目的在于鼓励价值网络的预测趋近于 TD 目标。理想情况下,
\(q(s_j,a_j;w)=r_j+\gamma \cdot Q(s_{j+1},\mu(s_{j+1};\theta_{now});w_{now}), \quad \forall (s_j,a_j,r_j,s_{j+1}).\)
在收集经验的过程中,行为策略决定了如何基于\(s_j\)生成\(a_j\),然而这不重要。上面的公式只希望等式左边去拟合等式右边,而不在乎\(a_j\)是如何生成的。
从价值学习的角度看待 DPG
假如我们知道最优动作价值函数\(Q^{\star}(s,a;w)\),我们可以这样做决策:给定当前状态\(s_t\),选择最大化 Q 值的动作
\(a_t=\arg\max_{a \in A} Q^{\star}(s_t,a)\).
DQN 记作\(Q(s,a;w)\),它是\(Q^{\star}(s,a;w)\)的函数近似。训练 DQN 的目的是让\(Q(s,a;w)\)趋近\(Q^{\star}(s,a;w)\),\(\forall s \in S, a \in A\)。在训练好 DQN 之后,可以这样做决策:
\(a_t=\arg\max_{a \in A} Q(s_t,a;w).\)
如果动作空间\(A\)是离散集合,那么上述最大化很容易实现。可是如果\(A\)是连续集合,则很难对\(Q\)求最大化。
可以把 DPG 看做对最优动作价值函数\(Q^{\star}(s,a)\)的另一种近似方式,用于连续控制问题。我们希望学到策略网络\(\mu(s;\theta)\)和价值网络\(q(s,a;w)\), 使得
\(q(s,\mu(s;\theta);w) \approx \max_{a \in A} Q^{\star}(s,a), \quad \forall s \in S.\)
我们可以把\(\mu\)和\(q\)看做是\(Q^{\star}\)的近似分解,而这种分解的目的在于方便做决策:
\(a_t = \mu(s_t;\theta) \approx \arg\max_{a \in A} Q^{\star}(s_t,a).\)
DPG 的高估问题
在之前的笔记 深度强化学习(王树森)笔记08-CSDN博客,我们讨过 DQN 的高估问题:如果用 Q 学习算法训练 DQN, 则 DQN 会高估真实最优价值函数\(Q^{\star}\)。把 DQN 记作\(Q(s,a;w)\)。如果用 Q 学习算法训练 DQN, 那么 TD 目标是
\(\hat{y}_j=r_j+\gamma \cdot \max_{a \in A} Q(s_{j+1},a;w).\)
之前得出结论:如果\(Q(s,a;w)\)是最优动作价值函数\(Q^{\star}(s,a)\)的无偏估计,那么\(\hat{y}_j\)是对\(Q^{\star}(s_j,a_j)\)的高估。用\(\hat{y}_j\)作为目标去更新 DQN, 会导致\(Q(s_j,a_j;w)\)高估\(Q^{\star}(s_j,a_j)\)。另一个结论是自举会导致高估的传播,造成高估越来越严重。
DPG 也存在高估问题,用上一节的算法训练出的价值网络\(q(s,a;w)\)会高估真实动作价值\(Q_{\pi}(s,a)\)。造成 DPG 高估的原因与 DQN 类似:第一,TD 目标是对真实动作价值的高估;第二,自举导致高估的传播。下面具体分析两个原因;如果读者不感兴趣,只需要记住上述结论即可,可以跳过下面的内容。
最大化造成高估:
训练策略网络的时候,我们希望策略网络计算出的动作\(\hat{a}=a=\mu(s;\theta)\)能得到价值网络尽量高的评价,也就是让\(q(s,\hat{a};w)\)尽量大。我们通过求解下面的优化模型来学习策略网络:
\(\theta^{\star}=\operatorname{argmax}_{\theta}\mathbb{E}_S[q(S,\hat{A};w)], \quad \text{s.t.} \quad \hat{A}=\mu(S;\theta).\)
这个公式的意思是\(\mu(s;\theta^{\star})\)是最优的确定策略网络。 上面的公式与下面的公式意义相同(虽然不严格等价):
\(\mu(s;\theta^{\star})=\arg\max_{a \in A} q(s,a;w), \quad \forall s \in S.\)
这个公式的意思也是\(\mu(s;\theta^{\star})\)是最优的确定策略网络。训练价值网络\(q\)时用的 TD 目标是
\(\begin{align*} \widehat{y}_{j} &= r_{j} + \gamma \cdot q\left(s_{j+1}, \mu\left(s_{j+1}; \theta\right); w\right) \\ &\approx r_{j} + \gamma \cdot \max_{a_{j+1}} q\left(s_{j+1}, a_{j+1}; w\right). \end{align*}\)
根据前面的分析,上面公式中的\(\max\)会导致\(\hat{y}_j\)高估真实动作价值\(Q_{\pi}(s_j,a_j)\)。在训练\(q\)时,我们把\(\hat{y}_j\)作为目标,鼓励价值网络\(q(s_j,a_j;w)\)接近\(\hat{y}_j\), 这会导致\(q(s_j,a_j;w)\)高估真实动作价值。
自举造成偏差传播:
前面的笔记中讨论过自举(bootstrapping)造成偏差的传播。
TD 目标
\(\hat{y}_j = r_j + \gamma \cdot q(s_{j+1},\mu(s_{j+1};\theta);w)\)
是用价值网络算出来的,而它又被用于更新价值网络\(q\)本身,这属于自举。假如价值网络\(q(s_{j+1},a_{j+1};\theta)\)高估了真实动作价值\(Q_{\pi}(s_{j+1},a_{j+1})\),那么 TD 目标\(\hat{y}_j\)则是对\(Q_{\pi}(s_j,a_j)\)的高估,这会导致\(q(s_j,a_j;w)\)高估\(Q_{\pi}(s_j,a_j)\)。自举让高估从\((s_{j+1},a_{j+1})\)传播到\((s_j,a_j)\)。
双延时确定策略梯度 (TD3)
由于存在高估等问题,DPG 实际运行的效果并不好。本节介绍的 Twin Delayed Deep Deterministic Policy Gradient (TD3) 可以大幅提升算法的表现,把策略网络和价值网络训练得更好。注意,本节只是改进训练用的算法,并不改变神经网络的结构。
高估问题的解决方案
解决方案——目标网络:
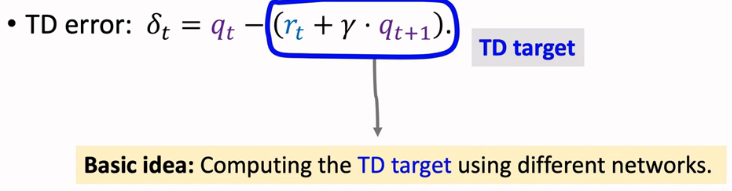
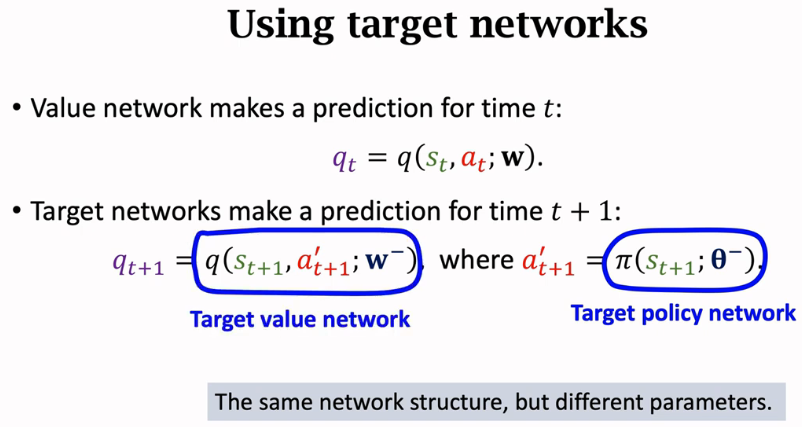
为了解决自举和最大化造成的高估,我们需要使用目标网络 (Target Networks)
计算 TD 目标\(\hat{y}_j\)。训练中需要两个目标网络:
\(q(s,a;w^-)\)和\(\mu(s;\theta^-)\).
它们与价值网络、策略网络的结构完全相同,但是参数不同。TD 目标是用目标网络算的:
\(\hat{y}_j = r_j + \gamma \cdot q(s_{j+1},\hat{a}_{j+1};w^-), \quad \text{其中} \quad \hat{a}_{j+1}=\mu(s_{j+1};\theta^-).\)
把\(\hat{y}_j\)作为目标,更新\(w\),鼓励\(q(s_j,a_j;w)\)接近\(\hat{y}_j\)。四个神经网络之间的关系如图 10.7所示。
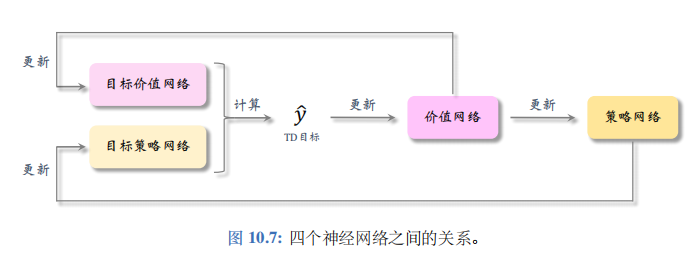
这种方法可以在一定程度上缓解高估,但是实验表明高估仍然很严重。
更好的解决方案——截断双 Q 学习 (clipped double
Q-learning):
这种方法使用两个价值网络和一个策略网络:
\(q(s,a;w_1)\),\(q(s,a;w_2)\),\(\mu(s;\theta)\).
三个神经网络各对应一个目标网络:
\(q(s,a;w_1^-)\),\(q(s,a;w_2^-)\),\(\mu(s;\theta^-)\).
用目标策略网络计算动作:
\(\hat{a}_{j+1}^-=\mu(s_{j+1};\theta^-),\)
然后用两个目标价值网络计算:
\(\hat{y}_{j,1} = r_j + \gamma \cdot q(s_{j+1},\hat{a}_{j+1}^-;w_1^-),\)
\(\hat{y}_{j,2} = r_j + \gamma \cdot q(s_{j+1},\hat{a}_{j+1}^-;w_2^-).\)
取两者较小者为TD 目标:
\(\hat{y}_j = \min\{\hat{y}_{j,1}, \hat{y}_{j,2}\}.\)
截断双 Q 学习中的六个神经网络的关系如图 10.8 所示。
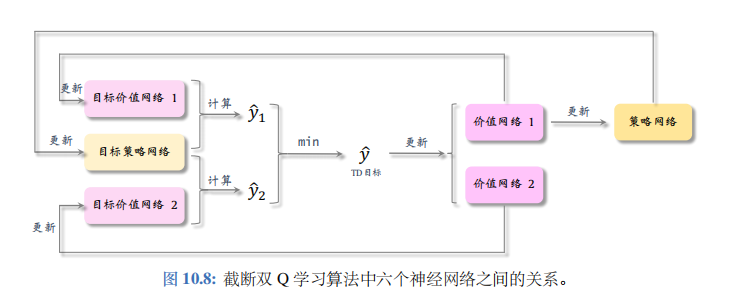
其他改进方法
可以在截断双 Q 学习算法的基础上做两处小的改进、进一步提升算法的表现。两种改进分别是往动作中加噪声、减小更新策略网络和目标网络的频率。
往动作中加噪声:
上一小节中截断双 Q 学习用目标策略网络计算动作:
\(\hat{a}_{j+1}^-=\mu(s_{j+1};\theta^-).\)
把这一步改成:
\(\hat{a}_{j+1}^-=\mu(s_{j+1};\theta^-)+\xi.\)
公式中的\(\xi\)是个随机向量,表示噪声,它的每一个元素独立随机从截断正态分布\(\mathcal{CN}(0,\sigma^2,-c,c)\)中抽取。把截断正态分布记作\(\mathcal{CN}(0,\sigma^2,-c,c)\),意思是均值为零,标准差为\(\sigma\)的正态分布,但是变量落在区间\([-c,c]\)之外的概率为零。正态分布与截断正态分布的对比如图 10.9 所示。使用截断正态分布,而非正态分布,是为了防止噪声\(\xi\)过大。使用截断,保证噪声大小不会超过 -c 和 c。
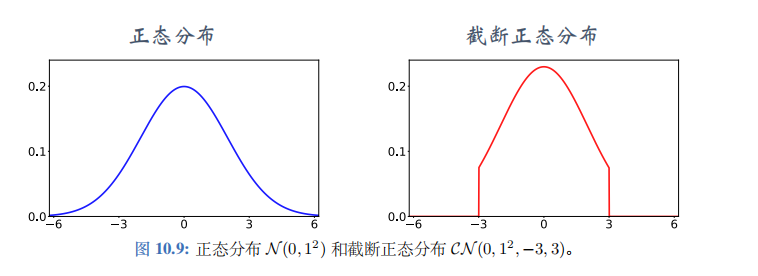
减小更新策略网络和目标网络的频率:
Actor-critic 用价值网络来指导策略网络的更新。如果价值网络 q
本身不可靠,那么用价值网络 q
给动作打的分数是不准确的,无助于改进策略网络\(\mu\)。在价值网络 q
还很差的时候就急于更新\(\mu\),
非但不能改进\(\mu\),反而会由于\(\mu\)的变化导致 q 的训练不稳定。
实验表明,应当让策略网络\(\mu\)以及三个目标网络的更新慢于价值网络\(q\)。传统的actor-critic
的每一轮训练都对策略网络、价值网络、以及目标网络做一次更新。更好的方法是每一轮更新一次价值网络,但是每隔\(k\)轮更新一次策略网络和三个目标网络。\(k\)是超参数,需要调。
训练流程
本节介绍了三种技巧,改进 DPG 的训练。第一,用截断双 Q 学习,缓解价值网络的高估。第二,往目标策略网络中加噪声,起到平滑作用。第三,降低策略网络和三个目标网络的更新频率。使用这三种技巧的算法被称作双延时确定策略梯度 (twin delayed deep deterministic policy gradient), 缩写是 TD3。
TD3 与 DPG 都属于异策略 (off-policy), 可以用任意的行为策略收集经验,事后做经验回放训练策略网络和价值网络。收集经验的方式与原始的训练算法相同,用\(\mu(s_t;\theta)+\epsilon\)与环境交互,把观测到的四元组\((s_t,a_t,r_t,s_{t+1})\)存入经验回放数组。
初始的时候,策略网络和价值网络的参数都是随机的。这样初始化目标网络的参数:
\(w_1^- \leftarrow w_1, \quad w_2^- \leftarrow w_2, \quad \theta^- \leftarrow \theta.\)
训练策略网络和价值网络的时候,每次从数组中随机抽取一个四元组,记作\((s_j,a_j,r_j,s_{j+1})\)。用下标 now 表示神经网络当前的参数,用下标 new 表示更新后的参数。然后执行下面的步骤,更新价值网络、策略网络、目标网络。
- 让目标策略网络做预测:
${j+1}-=(s_{j+1};-{now})+. $
其中向量\(\xi\)的每个元素都独立从截断正态分布\(\mathcal{CN}(0,\sigma^2,-c,c)\)中抽取.
- 让两个目标价值网络做预测:
\(\hat{q}_{1,j+1}^-=q(s_{j+1},\hat{a}_{j+1}^-;w_{1,now}^-) \quad \text{和} \quad \hat{q}_{2,j+1}^-=q(s_{j+1},\hat{a}_{j+1}^-;w_{2,now}^-).\)
- 计算 TD 目标:
\(\hat{y}_j = r_j + \gamma \cdot \min\{\hat{q}_{1,j+1}^-, \hat{q}_{2,j+1}^-\}.\)
- 让两个价值网络做预测:
\(\hat{q}_{1,j}=q(s_j,a_j;w_{1,now}) \quad \text{和} \quad \hat{q}_{2,j}=q(s_j,a_j;w_{2,now}).\)
- 计算 TD 误差:
\(\delta_{1,j}=\hat{q}_{1,j}-\hat{y}_j \quad \text{和} \quad \delta_{2,j}=\hat{q}_{2,j}-\hat{y}_j.\)
- 更新价值网络:
\(w_{1,new} \leftarrow w_{1,now} - \alpha \cdot \delta_{1,j} \cdot \nabla_w q(s_j,a_j;w_{1,now}),\)
\(w_{2,new} \leftarrow w_{2,now} - \alpha \cdot \delta_{2,j} \cdot \nabla_w q(s_j,a_j;w_{2,now}).\)
- 每隔\(k\)轮更新一次策略网络和三个目标网络:
- 让策略网络做预测:
\(\hat{a}_j=\mu(s_j;\theta_{now}). \quad \text{然后更新策略网络:}\)
\(\theta_{new} \leftarrow \theta_{now} + \beta \cdot \nabla_{\theta}\mu(s_j;\theta_{now}) \cdot \nabla_a q(s_j,\hat{a}_j;w_{1,now}).\)
- 更新目标网络的参数:
\(\theta_{new}^- \leftarrow \tau \cdot \theta_{new} + (1-\tau) \cdot \theta_{now}^-,\)
\(w_{1,new}^- \leftarrow \tau \cdot w_{1,new} + (1-\tau) \cdot w_{1,now}^-,\)
\(w_{2,new}^- \leftarrow \tau \cdot w_{2,new} + (1-\tau) \cdot w_{2,now}^-.\)
随机高斯策略
上一节用确定策略网络解决连续控制问题。本节用不同的方法做连续控制,本节的策略网络是随机的,它是随机正态分布 (也叫高斯分布)。
基本思路
我们先研究最简单的情形:自由度等于 1, 也就是说动作\(a\)是实数,动作空间\(A \subset \mathbb{R}\)。把动作的均值记作\(\mu(s)\),标准差记作\(\sigma(s)\), 它们都是状态\(s\)的函数。用正态分布的概率密度函数作为策略函数:\(\pi(a|s)=\frac{1}{\sqrt{6.28}\cdot\sigma(s)}\cdot\exp\left(-\frac{(a-\mu(s))^2}{2\cdot\sigma^2(s)}\right). \quad (10.2)\)
假如我们知道函数\(\mu(s)\)和\(\sigma(s)\)的解析表达式,可以这样做控制:
- 观测到当前状态\(s\), 预测均值\(\widehat{\mu} = \mu(s)\)和标准差\(\widehat{\sigma} = \sigma(s).\)。
- 从正态分布中做随机抽样\(a \sim N(\mu^,\sigma^2)\); 智能体执行动作\(a\)。
然而我们并不知道\(\mu(s)\)和\(\sigma(s)\)是怎么样的函数。一个很自然的想法是用神经网络来近似这两个函数。把神经网络记作\(\mu(s;\theta)\)和\(\rho(s;\theta)\),其中\(\theta\)表示神经网络中的可训练参数。但实践中最好不要直接近似标准差\(\sigma\),而是近似方差对数\(\ln \sigma^2\)。定义两个神经网络:
\(\mu(s;\theta) \quad \text{和} \quad \rho(s;\theta),\)
分别用于预测均值和方差对数。可以按照图10.10来搭建神经网络。
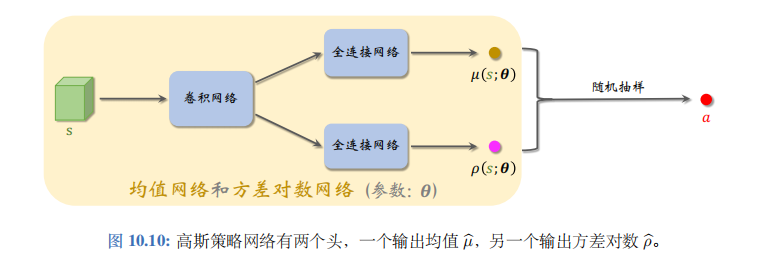
神经网络的输入是状态\(s\),通常是向量、矩阵或者张量。神经网络有两个输出头,分别记作\(\mu(s;\theta)\)和\(\rho(s;\theta)\)可以这样用神经网络做控制:
- 观测到当前状态\(s\), 计算均值\(\widehat{\mu} = \mu(s;\theta)\), 方差对数\(\widehat{\rho} = \rho(s;\theta)\), 以及方差$ ^2 = ()$.
- 从正态分布中做随机抽样:\(a \sim \mathcal{N}(\widehat{\mu}, \widehat{\sigma}^2)\); 智能体执行动作\(a\).
用神经网络近似均值和标准差之后,公式 (10.2) 中的策略函数\(\pi(a|s)\)变成了下面的策略网络:
\(\pi(a|s;\theta)=\frac{1}{\sqrt{6.28\cdot\exp[\rho(s;\theta)]}}\cdot\exp\left(-\frac{(a-\mu(s;\theta))^2}{2\cdot\exp[\rho(s;\theta)]}\right).\)
实际做控制的时候,我们只需要神经网络\(\mu(s;\theta)\)和\(\rho(s;\theta)\),用不到真正的策略网络\(\pi(a|s;\theta)\).
随机高斯策略网络
上一小节假设控制问题的自由度是\(d=1\),也就是说动作\(a\)是标量。实际问题中的自由度\(d\)往往大于 1, 那么动作\(a\)是\(d\)维向量。对于这样的问题,我们修改一下神经网络结构,让两个输出\(\mu(s;\theta)\)和\(\rho(s;\theta)\)都\(d\)维向量;见图10.11。
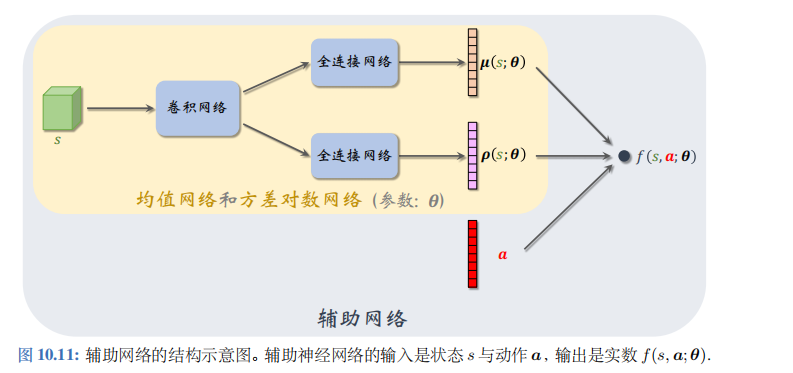
用标量\(a_i\)表示动作向量\(a\)的第\(i\)个元素。用函数\(\mu_i(s;\theta)\)和\(\rho_i(s;\theta)\)分别表示\(\mu(s;\theta)\)和\(\rho(s;\theta)\)的第\(i\)个元素。我们用下面这个特殊的多元正态分布的概率密度函数作为策略网络:
\(\pi(a|s;\theta)=\prod_{i=1}^{d}\frac{1}{\sqrt{6.28\cdot\exp[\rho_i(s;\theta)]}}\cdot\exp\left(-\frac{(a_i-\mu_i(s;\theta))^2}{2\cdot\exp[\rho_i(s;\theta)]}\right).\)
做控制的时候只需要均值网络\(\mu(s;\theta)\)和方差对数网络\(\rho(s;\theta)\),不需要策略网络\(\pi(a|s;\theta)\)做训练的时候也不需要\(\pi(a|s;\theta)\), 而是要用辅助网络\(f(s,a;\theta)\)。总而言之,策略网络\(\pi\)只是帮助你理解本节的方法而已,实际算法中不会出现\(\pi\)。
图10.11描述了辅助网络\(f(s,a;\theta)\)与\(\mu\)、\(\rho\)、\(a\)的关系。辅助网络具体是这样定义的:
\(f(s,a;\theta)=-\frac{1}{2}\sum_{i=1}^{d}\left(\rho_i(s;\theta)+\frac{(a_i-\mu_i(s;\theta))^2}{\exp[\rho_i(s;\theta)]}\right).\)
它的可训练参数\(\theta\)都是从\(\mu(s;\theta)\)和\(\rho(s;\theta)\)中来的。不难发现,辅助网络与策略网络有这样的关系:
\(f(s,a;\theta)=\ln\pi(a|s;\theta)+\text{Constant}. \quad (10.3)\)
策略梯度
回忆一下之前学过的内容。在\(t\)时刻的折扣回报记作随机变量\(U_t=R_t+\gamma \cdot R_{t+1}+\gamma^2 \cdot R_{t+2}+\cdots+\gamma^{n-t} \cdot R_n\).
动作价值函数\(Q_{\pi}(s_t,a_t)\)是对折扣回报\(U_t\)的条件期望。前面章节推导过策略梯度的蒙特卡洛近似:
\(g=Q_{\pi}(s,a) \cdot \nabla_{\theta}\ln\pi(a|s;\theta).\)
由公式 (10.3) 可得:
\(g=Q_{\pi}(s,a) \cdot \nabla_{\theta}f(s,a;\theta). \quad (10.4)\)
有了策略梯度,就可以学习参数\(\theta\)。训练的过程大致如下:
搭建均值网络\(\mu(s;\theta)\)、方差对数网络\(\rho(s;\theta)\)、辅助网络\(f(s,a;\theta)\)。
让智能体与环境交互,记录每一步的状态、动作、奖励,并对参数\(\theta\)做更新:
(a). 观测到当前状态\(s\),计算均值、方差对数、方差:\(\hat{\mu}=\mu(s;\theta)\),\(\hat{\rho}=\rho(s;\theta)\),\(\hat{\sigma}^2=\exp(\hat{\rho})\).
此处的指数函数\(\exp(\cdot)\)应用到向量的每一个元素上。
(b). 设\(\hat{\mu}_i\)和\(\hat{\sigma}_i\)分别是\(d\)维向量\(\hat{\mu}\)和\(\hat{\sigma}\)的第\(i\)个元素。从正态分布中做抽样:\(a_i \sim N(\hat{\mu}_i,\hat{\sigma}_i^2)\),\(\forall i=1,\cdots,d\). 把得到的动作记作\(a=[a_1,\cdots,a_d]\).
(c). 近似计算动作价值:\(\hat{q} \approx Q_{\pi}(s,a)\).
(d). 用反向传播计算出辅助网络关于参数\(\theta\)的梯度:\(\nabla_{\theta}f(s,a;\theta)\).
(e). 用策略梯度上升更新参数:\(\theta \leftarrow \theta + \beta \cdot \hat{q} \cdot \nabla_{\theta}f(s,a;\theta)\). 此处的\(\beta\)是学习率。
用 REINFORCE 学习参数
REINFORCE 用实际观测的折扣回报\(u_t=\sum_{k=t}^n\gamma^{k-t} \cdot r_k\)代替动作价值\(Q_{\pi}(s_t,a_t)\)。
道理是这样的。动作价值是回报的期望:
\(Q_{\pi}(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]\).
随机变量\(U_t\)的一个实际观测值\(u_t\)是期望的蒙特卡洛近似。这样一来,公式 (10.4) 中的策略梯度就能近似成\(g \approx u_t \cdot \nabla_{\theta}f(s,a;\theta)\).
在搭建好均值网络\(\mu(s;\theta)\)、方差对数网络\(\rho(s;\theta)\)、辅助网络\(f(s,a;\theta)\)之后,我们用REINFORCE 更新参数\(\theta\)。设当前参数为\(\theta_{now}\)。REINFORCE 重复以下步骤,直到收敛:
- 用\(\mu(s;\theta_{now})\)和\(\rho(s;\theta_{now})\)控制智能体与环境交互,完成一局游戏,得到一条轨迹\(s_1,a_1,r_1,s_2,a_2,r_2,\cdots,s_n,a_n,r_n\).
- 计算所有的回报:\(u_t=\sum_{k=t}^T\gamma^{k-t} \cdot r_k, \quad \forall t=1,\cdots,n\).
- 对辅助网络做反向传播,得到所有的梯度:\(\nabla_{\theta}f(s_t,a_t;\theta_{now}), \quad \forall t=1,\cdots,n\).
- 用策略梯度上升更新参数:\(\theta_{new} \leftarrow \theta_{now} + \beta \cdot \sum_{t=1}^{n}\gamma^{t-1} \cdot u_t \cdot \nabla_{\theta}f(s_t,a_t;\theta_{now})\).
上述算法标准的 REINFORCE, 效果不如使用基线的 REINFORCE。可以用基线改进上面描述的算法。REINFORCE 算法属于同策略(on-policy),不能使用经验回放。
用 Actor-Critic 学习参数
Actor-critic 需要搭建一个价值网络\(q(s,a;w)\), 用于近似动作价值函数\(Q_{\pi}(s,a)\)。价值网络的结构如图 10.12 所示。此外,还需要一个目标价值网络\(q(s,a;w^-)\), 网络结构相同,但是参数不同。
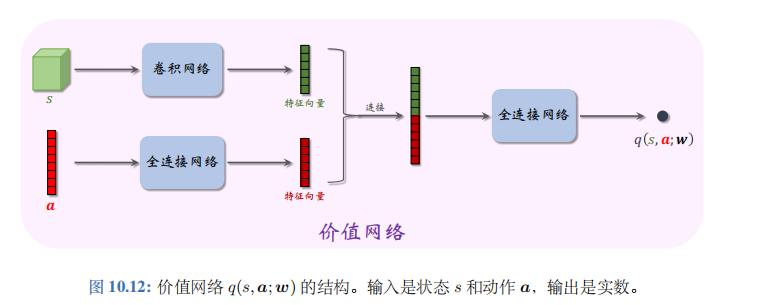
在搭建好均值网络\(\mu\)、方差对数网络\(\rho\)、辅助网络\(f\)、价值网络\(q\)之后,我们用 SARSA 算法更新价值网络参数\(w\), 用近似策略梯度更新控制器参数\(\theta\)。设当前参数为\(w_{now}\)和\(\theta_{now}\)。重复以下步骤更新价值网络参数、控制器参数,直到收敛:
- 实际观测到当前状态\(s_t\),用控制器算出均值\(\mu(s_t;\theta_{now})\)和方差对数\(\rho(s_t;\theta_{now})\),然后随机抽样得到动作\(a_t\)。智能体执行动作\(a_t\), 观测到奖励\(r_t\)与新的状态\(s_{t+1}\)。
- 计算均值\(\mu(s_{t+1};\theta_{now})\)和方差对数\(\rho(s_{t+1};\theta_{now})\),然后随机抽样得到动作\(\tilde{a}_{t+1}\)。这个动作只是假想动作,智能体不予执行。
- 用价值网络计算出:\(\hat{q}_t=q(s_t,a_t;w_{now})\).
- 用目标网络计算出:\(\hat{q}_{t+1}=q(s_{t+1},\tilde{a}_{t+1};w_{now}^-)\).
- 计算 TD 目标和 TD 误差:\(\hat{y}_t=r_t+\gamma \cdot \hat{q}_{t+1}\),\(\delta_t=\hat{q}_t-\hat{y}_t\).
- 更新价值网络的参数:\(w_{new} \leftarrow w_{now} - \alpha \cdot \delta_t \cdot \nabla_w q(s_t,a_t;w_{now})\).
- 更新策略网络参数参数:\(\theta_{new} \leftarrow \theta_{now} + \beta \cdot \hat{q}_t \cdot \nabla_{\theta}f(s_t,a_t;\theta_{now})\).
- 更新目标网络参数:\(w_{new}^- \leftarrow \tau \cdot w_{new} + (1-\tau) \cdot w_{now}^-\).
算法中的\(\alpha\)、\(\beta\)、\(\tau\)都是超参数,需要手动调整。上述算法是标准的 actor-critic. 效果不如advantage actor-critic (A2C)。可以用A2C改进上述方法。
总结
离散控制问题的动作空间\(A\)是个有限的离散集,连续控制问题的动作空间\(A\)是个连续集。如果想将 DQN 等离散控制方法应用到连续控制问题,可以对连续动作空间做离散化,但这只适用于自由度较小的问题。
可以用确定策略网络\(a=\mu(s;\theta)\)做连续控制。网络的输入是状态\(s\), 输出是动作\(a\),\(a\)是向量,大小等于问题的自由度。
确定策略梯度 (DPG) 借助价值网络\(q(s,a;w)\)训练确定策略网络。DPG 属于异策略,用行为策略收集经验,做经验回放更新策略网络和价值网络。
DPG 与 DQN 有很多相似之处,而且它们的训练都存在高估等问题。TD3 使用几种技巧改进 DPG: 截断双 Q 学习、往动作中加噪声、降低更新策略网络和目标网络的频率。
可以用随机高斯策略做连续控制。用两个神经网络分别近似高斯分布的均值和方差对数,并用策略梯度更新两个神经网络的参数。