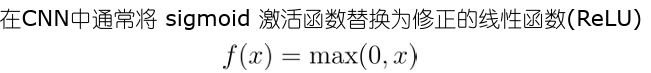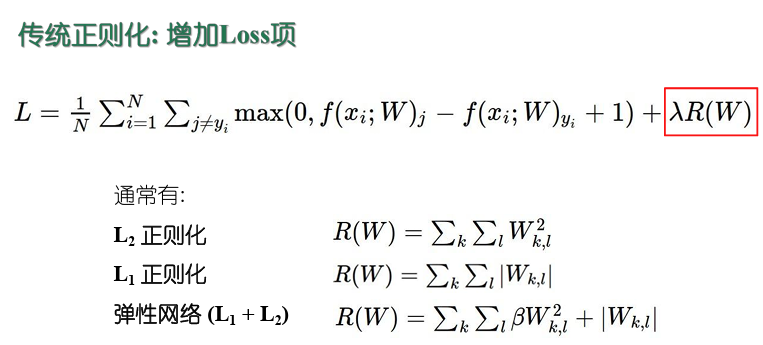11. 深度学习
- 神经网络
- 神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的反应
- 机器学习中的神经网络通常是指“神经网络学习”或者机器学习与神经网络两个学科的交叉部分
- 神经元模型
- M-P神经元模型
- 输入:来自其他个神经元传递过来的输入信号
- 处理:输入信号通过带权重的连接进行传递,神经元接受到总输入值将与神经元的阈值进行比较
- 输出:通过激活函数的处理以得到输出
- 激活函数
- 阶跃函数
- Sigmoid函数
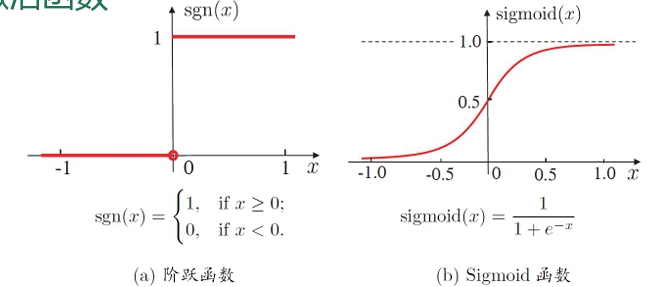
- 理想激活函数是阶跃函数,0表示抑制神经元而1表示激活神经元
- 阶跃函数具有不连续、不光滑等不好的性质,常用的是Sigmoid函数
- M-P神经元模型
- 感知机
- 感知机由两层神经元组成,输入层接受外界输入信号传递给输出层,输出层是M-P神经元(阈值逻辑单元)
- 感知机能够容易地实现逻辑与、或、非运算
- 感知机学习
- 给定训练数据集,权重w与阈值θ可以通过学习得到
- 感知机学习规则
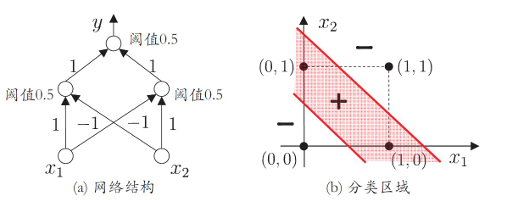
- 感知机求解与、或、非问题和异或问题
- 若两类模式线性可分,则感知机的学习过程一定会收敛;否则感知机的学习过程将会发生震荡
- 单层感知机的学习能力非常有限,只能解决线性可分问题
- 事实上,与、或、非问题是线性可分的,因此感知机学习过程能够求得适当的权值向量.而异或问题不是线性可分的,感知机学习不能求得合适解
- 多层感知机
- 解决异或问题的两层感知机
- 输出层与输入层之间的一层神经元,被称之为隐层或隐含层,隐含层和输出层神经元都是具有激活函数的功能神经元
- 多层前馈神经网络
- 定义:每层神经元与下一层神经元全互联,神经元之间不存在同层连接也不存在跨层连接
- 前馈:输入层接受外界输入,隐含层与输出层神经元对信号进行加工,最终结果由输出层神经元输出
- 学习:根据训练数据来调整神经元之间的“连接权”以及每个功能神经元的“阈值”
- 多层网络:包含隐层的网络
- 解决异或问题的两层感知机
- 误差逆传播算法
- 误差逆传播算法(ErrorBackPropagation,简称BP)是最成功的训练多层前馈神经网络的学习算法.
- BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整.对误差Ek,给定学习率n,学习率n∈(0,1)控制着算法每一轮迭代中的更新步长,若太长则让容易震荡,太小则收敛速度又会过慢

- 标准BP算法
- 每次针对单个训练样例更新权值与阈值.
- 参数更新频繁,不同样例可能抵消,需要多次迭代.
- 累计BP算法
- 但在很多任务中,累计误差下降到一定程度后,进一步下降会非常缓慢,这时标准BP算法往往会获得较好的解,尤其当训练集非常大时效果更明显.
- 多层前馈网络表示能力
- 只需要一个包含足够多神经元的隐层,多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数
- 多层前馈网络局限
- 神经网络由于强大的表示能力,经常遭遇过拟合,表现为:训练误差持续降低,但测试误差却可能上升
- 如何设置隐层神经元的个数仍然是个未决问题,实际应用中通常使用“试错法”调整
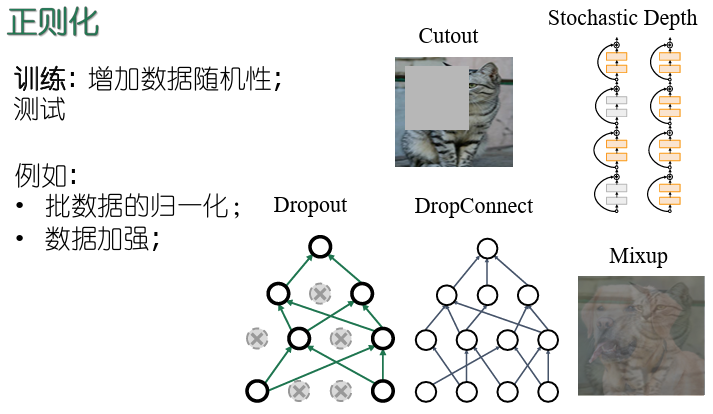
- 缓解过拟合的策略
- 早停:在训练过程中,若训练误差降低,但验证误差升高,则停止训练
- 正则化:在误差目标函数中增加一项描述网络复杂程度的部分,例如连接权值与阈值的平方和
- 全局最小与局部最小
- “跳出”局部最小的策略
- 基于梯度的搜索是使用最为广泛的参数寻优方法。如果误差函数仅有一个局部极小,那么此时找到的局部极小就是全局最小;然而,如果误差函数具有多个局部极小,则不能保证找到的解是全局最小。在现实任务中,通常采用以下策略“跳出”局部极小,从而进一步达到全局最小。
- 多组不同的初始参数优化神经网络,选取误差最小的解作为最终参数;
- 模拟退火技术[AartsandKorst,1989]每一步都以一定的概率接受比当前解更差的结果,从而有助于跳出局部极小;
- 随机梯度下降与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素;
- 遗传算法[Goldberg,1989]遗传算法也常用来训练神经网络以更好地逼近全局极小
- “跳出”局部最小的策略
- 深度学习
- 深度学习模型
- 典型的深度学习模型就是很深层的神经网络
- 模型复杂度
- 增加隐层神经元的数目(模型宽度)
- 增加隐层数目(模型深度)
- 从增加模型复杂度的角度看,增加隐层的数目比增加隐层神经元的数目更有效,这是因为增加隐层数不仅增加拥有激活函数的神经元数目,还增加了激活函数嵌套的层数
- 复杂模型难点
- 多隐层网络难以直接用经典算法(例如标准BP算法)进行训练,因为误差在多隐层内逆传播时,往往会”发散”而不能收敛到稳定状态.
- 卷积神经网络CNN
- 卷积神经网络
- 卷积层:每个卷积层包含多个特征映射,每个特征映射是一个由多个神经元构成的“平面”,通过一种卷积滤波器提取的一种特征;
- 采样层(Pooling层):亦称“汇合层”,其作用是基于局部相关性原理进行亚采样,从而在减少数据量的同时保留有用信息;
- 连接层:每个神经元被全连接到输出层每个神经元,本质就是传统的神经网络,其目的是通过连接层和输出层的连接完成识别任务。
- 卷积神经网络
- 卷积神经网络激活函数
- 卷积神经网络训练
- CNN可以用BP进行训练,但在训练中,无论是卷积层还是采样层,每一组神经元都是用相同的连接权,从而大幅减少了需要训练的参数数目
- 复杂模型训练方法
- 权共享
- 一组神经元使用相同的连接权值
- 权共享策略在卷积神经网络(CNN)中发挥了重要作用
- 卷积神经网络
- 结构:CNN复合多个卷积层和采样层对输入信号进行加工,然后在连接层实现与输出目标之间的映射
- 权共享
- 深度复杂模型训练方法
- 预训练+微调
- 预训练:逐层训练是多隐层网络训练的有效手段,每次训练一层隐层结点,训练时将上一层隐层结点的输出作为输入,而本层隐结点的输出作为下一层隐结点的输入,这称为”预训练”;
- 微调:在预训练全部完成后,再对整个网络进行微调训练;微调一般使用BP算法。
- 例子:深度信念网络
- 结构:每一层都是一个受限Boltzmann机
- 训练方法:无监督预训练+BP微调
- 分析
- 预训练+微调的做法可以视为将大量参数分组,对每组先找到局部看起来比较好的设置,然后再基于这些局部较优的结果联合起来进行全局寻优.
- 预训练+微调
- 深度学习模型
- 其他常见深度神经网络
- RNN循环神经网络
- 隐层循环
- LSTM长短时记忆模型
- RNN有梯度消失的问题
- 很难处理长序列的数据
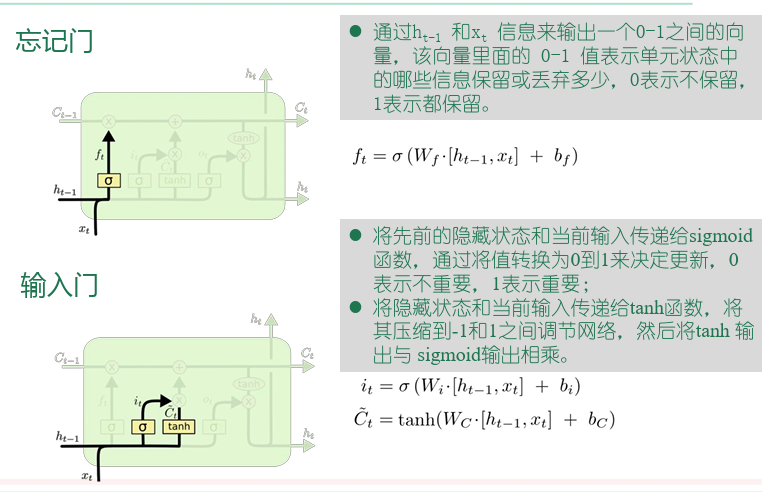
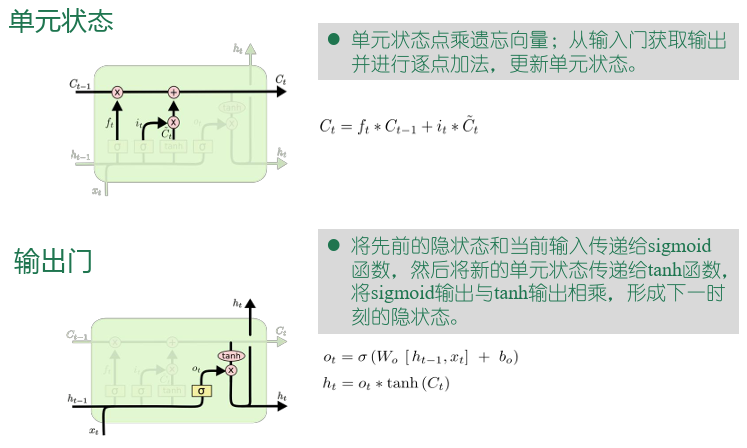
- LSTM由三个门来控制神经元状态,分别为忘记门、输入门和输出门
- 自编码器
- 限制性玻尔兹曼机
- 能量模型
- 神经网络中有一类模型为网络定义一个“能量”,能量最小化时网络达到理想状态,而网络的训练就是在最小化这个能量函数
- Boltzmann机
- Boltzmann机就是一种基于能量的模型
- 结构:显层与隐层
- 显层:数据的输入输出
- 隐层:数据的内在表达
- 神经元
- 布尔型,即只能取0和1两种状态,其中1表示激活,0表示抑制
- 网络中的神经元以任意不依赖于输入值的顺序进行更新,则网络最终将达到Boltzmann分布,此时状态向量出现的概率将仅由其能量与所有可能状态向量的能量确定:
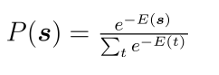
- Boltzmann机训练
- 将每个训练样本视为一个状态向量,使其出现的概率尽可能大
- 标准的Boltzmann机是一个全连接图,训练网络的复杂度很高,这使其难以用于解决现实任务
- 现实中常用受限Boltzmann机,简称RBM,RBM仅保留显层与隐层之间的连接,从而将Boltzmann机结构有完全图简化为二部图
- 受限Boltzmann机
- 能量模型
- 深度信念网络
- 生成模型
- VAE
- GAN
- RNN循环神经网络
- 梯度计算
- 数值梯度:近似,慢,容易计算;
- 解析梯度:准确,快,但是易于出错;
- 实际:通常采用解析梯度来计算,但是利用数值梯度做执行检查,被称为Gradientcheck
- 梯度消失与梯度爆炸
- 残差结构
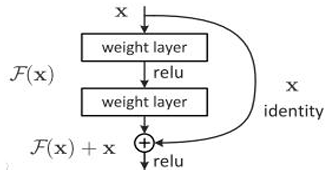
- ResNet
- 比CNN更容易训练,残差块使用了跳跃连接,可以缓解在深度神经网络中增加深度带来的梯度消失问题。
- Batchsize+BatchNormalization
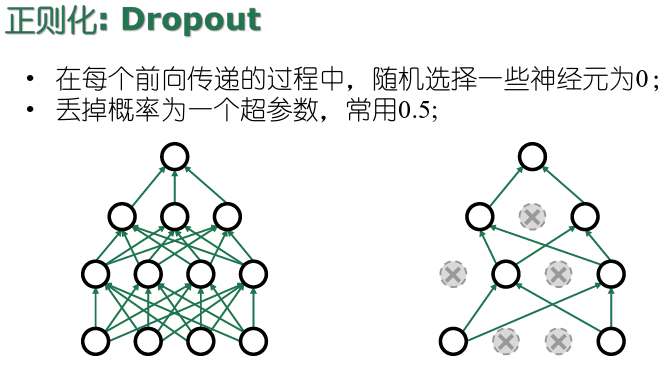
- 正则化

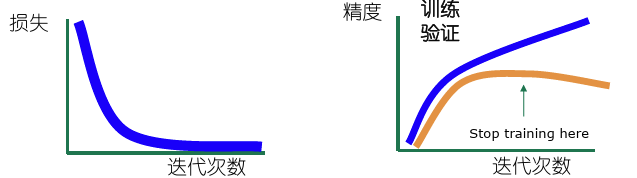
- 训练多久
- 当模型在验证集上精度下降时,停止训练;
- 或者训练很长的时间,但一直保存每步的训练结果,跟踪模型的训练过程
- 理解深度学习
- “特征工程”VS“特征学习”或者“表示学习”
- 特征工程由人类专家根据现实任务来设计,特征提取与识别是单独的两个阶段
- 特征学习通过深度学习技术自动产生有益于分类的特征,是一个端到端的学习框架。
- 特征工程由人类专家根据现实任务来设计,特征提取与识别是单独的两个阶段
- 函数拟合
- 只需要一个包含足够多神经元的隐层,多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数
- “特征工程”VS“特征学习”或者“表示学习”
11. 深度学习
http://binbo-zappy.github.io/2024/12/07/PR-ML/11-深度学习/