12. 强化学习

  1. 强化学习应用
    1. 两个应用
  2. 强化学习常用什么过程描述
    1. 马尔科夫性是什么
  3. 强化学习问题基本设置
    1. 机器所处环境E
    2. 状态空间：是机器感知到的环境的描述
    3. 机器能采取的行为空间A
    4. 策略(policy)π：X→A(或π：X×A→R)
    5. 潜在的状态转移(概率)函数Ｐ：X×X×A→R
    6. 潜在的奖赏(reward)函数Ｒ：X×X×A→R或Ｒ：X×X→R
    7. 强化学习对应四元组
      1. E=<X,A,P,R>
    8. 目标
      1. 机器通过在环境中不断尝试从而学到一个策略π，使得长期执行该策略后得到的累积奖赏最大
  4. 强化学习vs监督学习
    1. 监督学习：给有标记样本
    2. 强化学习：没有标记样本，通过执行动作之后反馈的奖赏来学习，强化学习在某种意义上可以认为是具有“延迟标记信息”的监督学习
  5. K-摇臂赌博机
    1. 特点
      1. 只有一个状态，K个动作
      2. 每个摇臂的奖赏服从某个期望未知的分布
      3. 执行有限次动作
      4. 最大化累积奖赏
    2. 探索-利用(Exploration-Exploitation)
      1. 探索：估计不同摇臂的优劣(奖赏期望的大小)
      2. 利用：选择当前最优的摇臂
    3. 在探索与利用之间进行折中
      1. e-贪心
        1. 以e的概率探索：均匀随机选择一个摇臂
        2. 以1-e的概率利用：选择当前平均奖赏最高的摇臂
      2. Softmax
  6. 有模型学习(model-basedlearning)
    1. E=<X,A,P,R>
      1. X,A,P,R均已知
      2. 方便起见，假设状态空间和动作空间均有限
    2. 强化学习的目标：找到使累积奖赏最大的策略π
    3. 策略评估：使用某策略所带来的累积奖赏
    4. 给定π，值函数的计算：值函数具有简单的递归形式
      1. Bellman等式
    5. 状态-动作值函数与状态值函数可以相互计算
    6. 贝尔曼方程
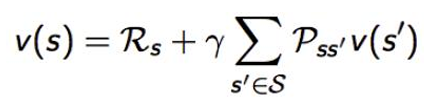
      2. 当前状态与下一状态价值函数之间的递归关系
    7. 策略评估
      2. 在模型已知时，对任意策略估计出有该策略带来的期望累积奖励——策略评估
    8. 策略评估：使用某策略所带来的期望累积奖赏；
    9. 策略改进：将非最优策略改进为最优策略
      1. 非最优策略的改进方式：将策略选择的动作改为当前最优的动作
    10. 策略迭代(policyiteration)：求解最优策略的方法
      1. 随机策略作为初始策略策略评估+策略改进+策略评估+策略改进+……直到策略收敛
      2. 策略迭代算法的缺点：每次改进策略后都要重新评估策略，导致耗时
    11. 值迭代
    12. 有模型学习小结
      1. 强化学习任务可归结为基于动态规划的寻优问题
      2. 与监督学习不同，这里并未涉及到泛化能力，而是为每一个状态找到最好的动作
  7. 免模型学习(model-freelearning)：更加符合实际情况
    1. 情况
      1. 转移概率，奖赏函数未知
      2. 甚至环境中的状态数目也未知
      3. 假定状态空间有限
    2. 免模型学习所面临的困难
      1. 策略无法评估
      2. 无法通过状态值函数计算状态-动作值函数
      3. 机器只能从一个起始状态开始探索环境
    3. 解决困难的办法
      1. 多次采样
      2. 直接估计每一对状态-动作的值函数
      3. 在探索过程中逐渐发现各个状态
    4. 蒙特卡罗强化学习：采样轨迹，用样本均值近似期望
      1. 策略评估：蒙特卡罗法
        1. 从某状态出发，执行某策略
        2. 对轨迹中出现的每对状态-动作，记录其后的奖赏之和
        3. 采样多条轨迹，每个状态-动作对的累积奖赏取平均
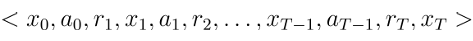
      2. 策略改进：换入当前最优动作
      3. 蒙特卡罗强化学习可能遇到的问题：轨迹的单一性
        1. 解决问题的办法
          2. 同策略蒙特卡罗强化学习算法
          3. 异策略蒙特卡罗强化学习算法
      4. 蒙特卡罗强化学习的缺点：低效
        1. 求平均时以“批处理式”进行
        2. 在一个完整的采样轨迹完成后才对状态-动作值函数进行更新
      5. 克服缺点的办法：时序差分(temporaldifference，TD)学习
    5. 时序差分学习
  8. 深度强化学习
    1. AlphaGo
  9. 强化学习应用
    1. AlphaGo
    2. 体彩世界杯
  10. 强化学习常用马尔可夫决策过程(MDP,MarkovDecisionProcess）描述
    1. 马尔科夫性：当前时刻的状态仅与前一时刻的状态和动作有关，与其他时刻的状态和动作条件独立
  11. 强化学习问题基本设置
    1. 机器所处环境E
      1. 例如在种西瓜任务中,环境是西瓜生长的自然世界
    2. 状态空间：是机器感知到的环境的描述
      1. 瓜苗长势的描述
    3. 机器能采取的行为空间A
      1. 浇水施肥等
    4. 策略(policy)π：X→A(或π：X×A→R)
      1. 根据瓜苗状态是缺水时，返回动作浇水
    5. 潜在的状态转移(概率)函数Ｐ：X×X×A→R
      1. 瓜苗当前状态缺水，选择动作浇水，有一定概率恢复健康，也有一定概率无法恢复
      2. 从一个状态到下一个状态的转移，要么为确定性转移过程，要么随机性转移过程
    6. 潜在的奖赏(reward)函数Ｒ：X×X×A→R或Ｒ：X×X→R
      1. 瓜苗健康对应奖赏+1，瓜苗凋零对应奖赏-10
    7. 强化学习对应四元组
      1. E=<X,A,P,R>
    8. 目标
      1. 机器通过在环境中不断尝试从而学到一个策略π，使得长期执行该策略后得到的累积奖赏最大
  12. 强化学习vs监督学习
    1. 监督学习：给有标记样本
    2. 强化学习：没有标记样本，通过执行动作之后反馈的奖赏来学习，强化学习在某种意义上可以认为是具有“延迟标记信息”的监督学习
  13. K-摇臂赌博机
    1. 特点
      1. 只有一个状态，K个动作
      2. 每个摇臂的奖赏服从某个期望未知的分布
      3. 执行有限次动作
      4. 最大化累积奖赏
    2. 探索-利用(Exploration-Exploitation)
      1. 探索：估计不同摇臂的优劣(奖赏期望的大小)
      2. 利用：选择当前最优的摇臂
    3. 在探索与利用之间进行折中
      1. e-贪心
        1. 以e的概率探索：均匀随机选择一个摇臂
        2. 以1-e的概率利用：选择当前平均奖赏最高的摇臂
      2. Softmax
        1. 基于当前已知的摇臂平均奖赏来对探索与利用折中
        2. 若某个摇臂当前的平均奖赏越大，则它被选择的概率越高,概率分配使用Boltzmann分布：
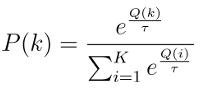
      3. 两种算法都有一个折中参数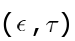，算法性能孰好孰坏取决于具体应用问题
  14. 有模型学习(model-basedlearning)
    1. E=<X,A,P,R>
      1. X,A,P,R均已知
      2. 方便起见，假设状态空间和动作空间均有限
    2. 强化学习的目标：找到使累积奖赏最大的策略π
    3. 策略评估：使用某策略所带来的累积奖赏
    4. 给定π，值函数的计算：值函数具有简单的递归形式
      1. Bellman等式
    5. 状态-动作值函数与状态值函数可以相互计算
    6. 贝尔曼方程
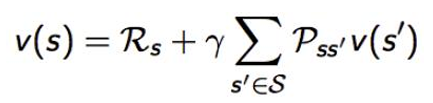
      2. 当前状态与下一状态价值函数之间的递归关系
    7. 策略评估
      2. 在模型已知时，对任意策略估计出有该策略带来的期望累积奖励——策略评估
    8. 策略评估：使用某策略所带来的期望累积奖赏；
    9. 策略改进：将非最优策略改进为最优策略
      1. 非最优策略的改进方式：将策略选择的动作改为当前最优的动作
    10. 策略迭代(policyiteration)：求解最优策略的方法
      1. 随机策略作为初始策略策略评估+策略改进+策略评估+策略改进+……直到策略收敛
      2. 策略迭代算法的缺点：每次改进策略后都要重新评估策略，导致耗时
    11. 值迭代
    12. 有模型学习小结
      1. 强化学习任务可归结为基于动态规划的寻优问题
      2. 与监督学习不同，这里并未涉及到泛化能力，而是为每一个状态找到最好的动作
  15. 免模型学习(model-freelearning)：更加符合实际情况
    1. 情况
      1. 转移概率，奖赏函数未知
      2. 甚至环境中的状态数目也未知
      3. 假定状态空间有限
    2. 免模型学习所面临的困难
      1. 策略无法评估
      2. 无法通过状态值函数计算状态-动作值函数
      3. 机器只能从一个起始状态开始探索环境
    3. 解决困难的办法
      1. 多次采样
      2. 直接估计每一对状态-动作的值函数
      3. 在探索过程中逐渐发现各个状态
    4. 蒙特卡罗强化学习：采样轨迹，用样本均值近似期望
      1. 策略评估：蒙特卡罗法
        1. 从某状态出发，执行某策略
        2. 对轨迹中出现的每对状态-动作，记录其后的奖赏之和
        3. 采样多条轨迹，每个状态-动作对的累积奖赏取平均
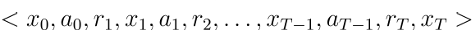
      2. 策略改进：换入当前最优动作
      3. 蒙特卡罗强化学习可能遇到的问题：轨迹的单一性
        1. 解决问题的办法
          2. 同策略蒙特卡罗强化学习算法
          3. 异策略蒙特卡罗强化学习算法
      4. 蒙特卡罗强化学习的缺点：低效
        1. 求平均时以“批处理式”进行
        2. 在一个完整的采样轨迹完成后才对状态-动作值函数进行更新
      5. 克服缺点的办法：时序差分(temporaldifference，TD)学习
    5. 时序差分学习
  16. 深度强化学习
    1. AlphaGo
AI > ML > PR & ML
#ML
12. 强化学习
http://binbo-zappy.github.io/2024/12/07/PR-ML/12-强化学习/
作者
Binbo
发布于
2024年12月7日
许可协议