8. SVM
- 将训练样本分开的超平面可能有很多,哪一个好呢?
- 应选择”正中间”,容忍性好,鲁棒性高,泛化能力最强
- 超平面方程
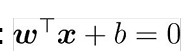
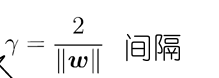
- svm基本型
- 最大间隔:寻找参数w和b,使得γ最大.
- 解的稀疏性

- 支持向量机解的稀疏性:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关.
- 核函数
- 难以知道显式的核映射函数基本想法:不显式地设计核映射,而是设计核函数

- 只要一个对称函数所对应的核矩阵半正定,则它就能作为核函数来使用
- 对于一个半正定核矩阵,总能找到一个与之对应的核映射;每一个核函数都隐式的定义了一个再生核希尔伯特空间的特征空间。
- 常用核函数
- 软间隔
- 现实中,很难确定合适的核函数使得训练样本在特征空间中线性可分;同时一个线性可分的结果也很难断定是否有过拟合造成的.
- 引入”软间隔”的概念,允许支持向量机在一些样本上不满足约束
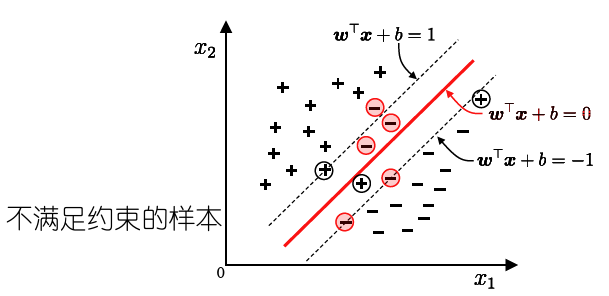
- 0/1损失函数
- 基本想法:最大化间隔的同时,让不满足约束的样本应尽可能少

- 存在的问题:0/1损失函数非凸、非连续,不易优化!
- 替代损失函数数学性质较好,一般是0/1损失函数的上界
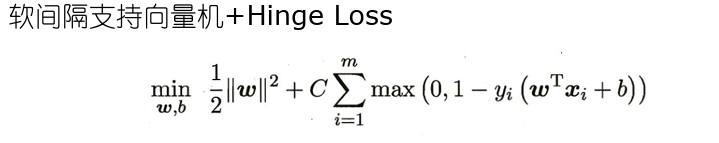

- 根据KKT条件可推得最终模型仅与支持向量有关,也即hinge损失函数依然保持了支持向量机解的稀疏性
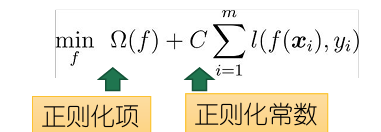
- 正则化
- 结构风险,描述模型的某些性质(超平面的间隔大小)
- 经验风险,描述模型与训练数据的契合程度,即训练集上的误差
- 通过替换上面两个部分,可以得到许多其他学习模型
- 对数几率回归(LogisticRegression)
- 最小绝对收缩选择算子(LASSO

- 软间隔支持向量机+对率损失
- 如果用对率损失函数来替代0/1损失函数,几乎就得到对率回归模型。
- 主要优势在于输出具有自然概率意义,即给出预测标记的同时也给出了概率;
- 如果用于多分类任务;SVM则需要进一步推广;
- 对率损失函数是光滑的单调递减函数,不能导出类似支持向量的概念;
- 对率回归的解依赖于更多的训练样本,其预测开销更大;
- SVM回归
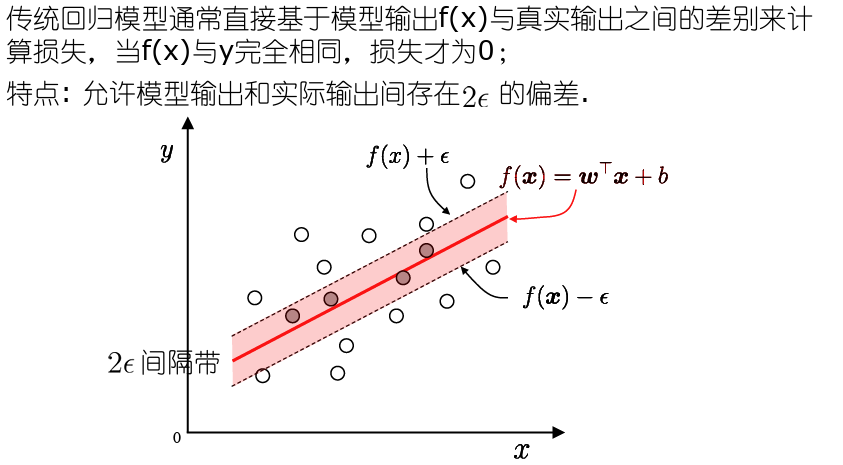
- 损失函数
- 落入中间间隔带的样本不计算损失,即被认为是预测正确,从而使得模型获得稀疏性.
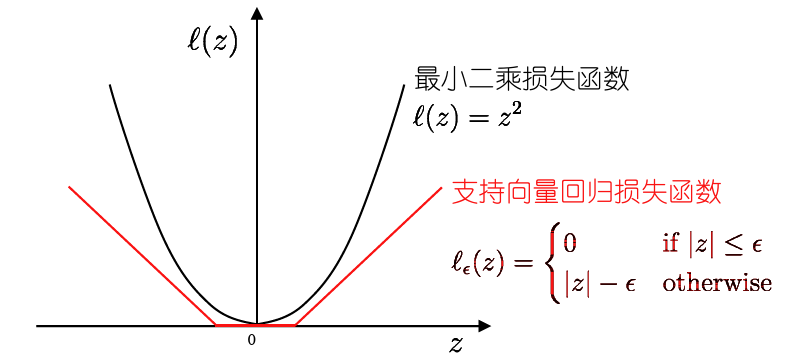
- 间隔带两侧的松弛程度可有所不同


- 核方法
- 无论是支持向量机还是支持向量回归,学得的模型总可以表示成核函数的线性组合
- 支持向量机的”最大间隔”思想
- 对偶问题及其解的稀疏性
- 通过向高维空间映射解决线性不可分的问题
- 引入”软间隔”缓解特征空间中线性不可分的问题
- 将支持向量的思想应用到回归问题上得到支持向量回归
- 将核方法推广到其他学习模型
8. SVM
http://binbo-zappy.github.io/2024/12/07/PR-ML/8-SVM/

