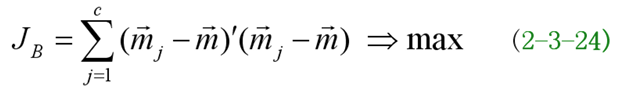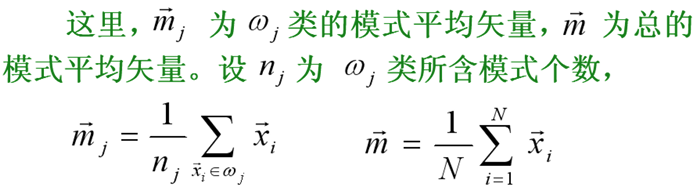9. 非监督学习
- 非监督学习
- 监督学习
- 根据一些给定的已知类别标号的样本,训练某种学习机器,使其能够对未知类别的样本进行分类
- 非监督学习
- 事先并不知道任何样本的类别标号,希望通过某种算法把一组未知类别的样本划分成若干类别。也称为聚类问题
- 监督学习
- 聚类分析
- 基本思想
- 相似的归为一类。
- 模式相似性的度量。
- 无监督分类算法。
- 特征量的类型
- 物理量:重量、长度、速度
- 次序量:等级、技能、学识
- 名义量:性别、状态、种类
- 基本思想
- 聚类过程遵循的基本步骤
- 特征选择
- 近邻测度
- 聚类准则
- 聚类算法
- 结果判定
- 模式相似性测度
- 用于描述各模式之间特征的相似程度
- 距离测度
- 欧氏距离
- 绝对值距离
- 马氏距离
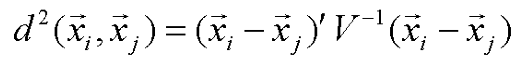
- 马氏距离对一切非奇异线性变换都是不变的,这说明它不受特征量纲选择的影响,并且是平移不变的。上面的V的含义是这个矢量集的协方差阵的统计量,故马氏距离加入了对特征的相关性的考虑。
- 相似测度
- 角度相似系数(夹角余弦
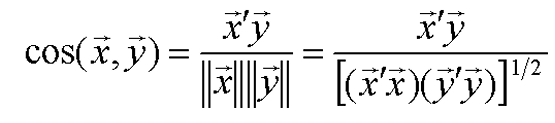
- 坐标系的旋转和尺度的缩放是不变的,但对一般的线形变换和坐标系的平移不具有不变性
- 相关系数
- 它实际上是数据中心化后的矢量夹角余弦。
- 角度相似系数(夹角余弦
- 匹配测度
- 距离测度
- 用于描述各模式之间特征的相似程度
- 类
- 类的定义
- 类的定义有很多种,类的划分具有人为规定性,这反映在定义的选取及参数的选择上。一个分类结果的优劣最后只能根据实际来评价。

- 类间距离测度方法
- 最近距离法
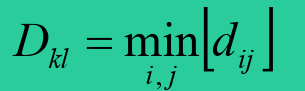
- 最远距离法
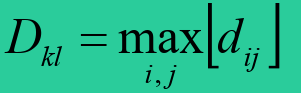
- 平均距离法
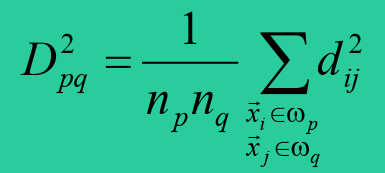
- 最近距离法
- 聚类的准则函数
- 判别分类结果好坏的一般标准:类内距离小,类间距离大。
- 类内距离准则
- c类mj为均值矢量
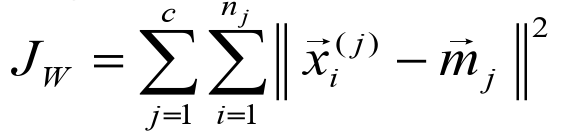
- 类间距离准则
- 基于类内距离类间距离的准则函数
- 类的定义
- 聚类算法
- 基于数据的方法
- 不尝试估计概率密度函数,直接从数据出发进行聚类
- 分类
- 按最小距离原则简单聚类方法
- 针对具体问题确定相似性阈值,将模式到各聚类中心间的距离与阈值比较,当大于阈值时该模式就作为另一类的类心,小于阈值时按最小距离原则将其分划到某一类中。
- 这类算法运行中模式的类别及类的中心一旦确定将不会改变。
- 按最小距离原则进行两类合并的方法
- 首先视各模式自成一类类合并成一类,,然后将距离最小的两不断地重复这个过程,直到成为两类为止。
- 这类算法运行中,类心不断地修正,但模式类别一旦指定后就不再改变,就是模式一旦划为一类后就不再被划分开,这类算法也称为分级聚类法。
- 依据准则函数动态聚类方法
- 设定一些分类的控制参数,定义一个能表征聚类结果优劣的准则函数,聚类过程就是使准则函数取极值的优化过程。
- 算法运行中,类心不断地修正,各模式的类别的指定也不断地更改。这类方法有C-均值法,ISODATA法等。
- 按最小距离原则简单聚类方法
- 类别分离的间接方法
- 动态聚类方法
- 聚类分析中,较普遍采用的方法
- 过程:
- 选择某种样本相似性度量(例如距离度量)
- 确定适当的聚类准则函数(评价聚类结果质量)
- 在初始分类基础上,用迭代算法,逐步优化聚类结果,使准则函数达极值(达最优聚类结果)
- 存在两个问题:
- 选代表点数目等于类别数目c。若c未知,则聚类过程中形成的类型数目是一个值得研究的问题
- 如何将所有样本分到以代表点为初始聚合中心的范围内,形成初始划分,即如何选取初始问题,是算法的另一关键问题
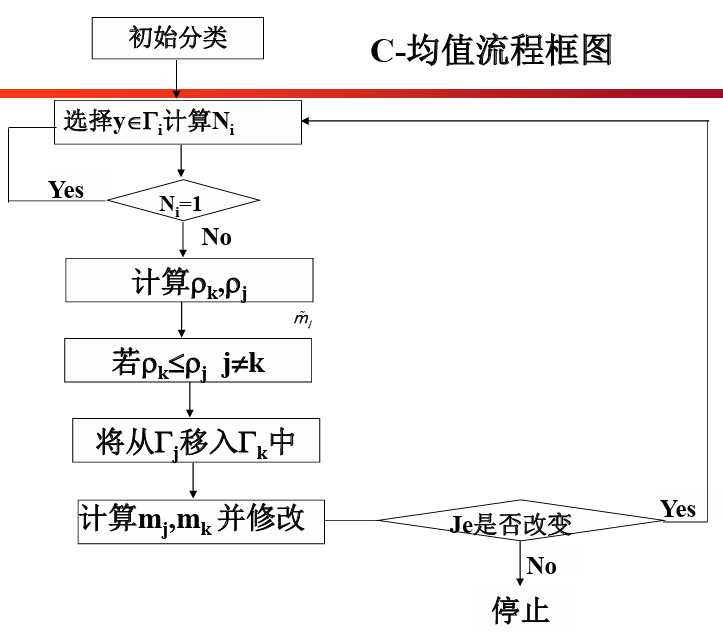
- C-均值算法(基于误差平方和准则Je)
- 优点:算法简单,实际中表现出色,是一种主要聚类方法
- 用样本间的距离作为相似性度量
- 用各类样本与类均值间的平方误差和作为聚类准则
- 基本思想:
- 取定c类,选取c个初始聚类中心,即代表点。按最小距离原则将各样本分配到离代表点最近的类中,不断重新计算类中心,调整各样本类别,最终使聚类准则函数Je最小。
- 算法步骤
- 任选取c个初始聚类中心(代表点)m1,m2,...,mc
- 计算每个样本与聚类中心(代表点)的距离,按最小距离原则将样本逐个归入相应一类,即
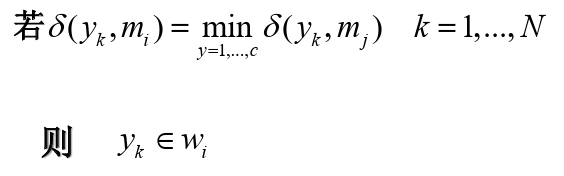
- 重新计算各类中心
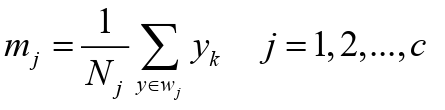
- 这一步是采取平均的方法来计算调整后的各类中心,且定为c类,故称为C-均值法。

- 调整分类
- 依据准则函数调整每个聚类中的每个样本。是否调整,由下式决定



- 若c未知,令c=1,2,3,...相应使用c-均值算法,则有Je随c增加而单调减小
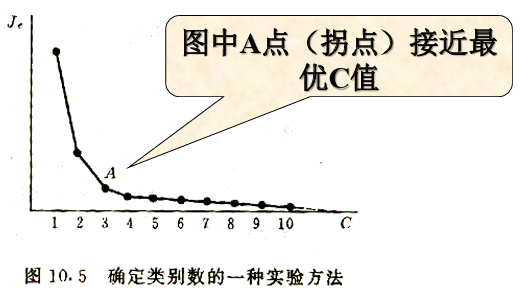

- ISODATA算法(迭代自组织数据分析算法)
- 与C-均值算法的相似之处:聚类中心都是通过样本均值的迭代运算来决定
- 与C-均值算法的区别:C-均值算法每次修改各类样本均值,计算太繁。ISODATA算法改为每次把全部样本都调整完毕后,才重新计算样本的均值
- C均值:ISODATA和合并逐个:样本修正法成批样本修正法,还增加了类的分裂合并功能。
- 步骤
- 设定初始聚类中心mi
- 将所有样本分给最近的聚类

- 修正各聚类中心值

- 计算所有样本对其相应聚类中心的总平均距离
- 判别分裂、合并及迭代运算等步骤



- 动态聚类方法
- 分级聚类方法
- 先把所有样本各自视作一类,逐级聚合类,“聚合法”。(合并成一agglomerative
- 先把所有样本视作一类本一类,“分解法),逐级分解为每一样”。(分裂divisive)
- n个混合样本,级聚合,∴先分为每级只把n类,依据相似性最大相似性大小,逐的两类聚合成一类形成一棵完整的树
- 关键问题:
- 如何选取类间相似性度量
- 聚合过程应停留在哪一级决定最后聚合成几类
- 若事先已知类型数目c,则应停留在n-c+1级上
- 若预先给定类间距离阈值D0,当类间距离大于阈值,则终止聚类过程
- 若c、D0均不知,先完成n→1全部聚类过程,然后根据类间相似性等,获取适当的聚类级作为最佳结果。
- 基于模型的方法
- 估计样本的概率密度函数
- 基于模型的方法:单峰子集分离法
- 基本假定:各类样本的分布是单峰的,根据总体分布中的单峰来划分子集
- 样本在整个特征空间中呈现两个分布高峰。
- 如果从分布的谷点将此特征空间划分为两个区则对应每个区域,样本分布就只有一个峰值这些区域被称为单峰区域。
- 每个单峰区域看作一个不同的决策域。落在同一单峰区域的待分类样本就被划分成同一类,称为单峰子类
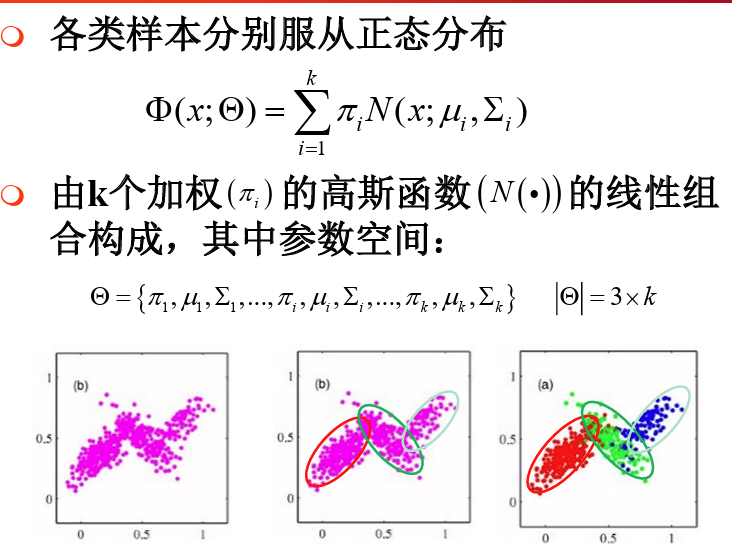
- 混合模型
- 高斯混合模型
- 混合模型参数估计
- 困难:
- 已知一个数据集,包含未知类别标号的样本但知道它们是从若干个服从不同分布的聚类中独立抽取出来的
- 要根据这些样本同时估计出各个聚类的概率密度函数.
- 非监督参数估计
- 非监督极大似然估计
- 理论上可解,但实际求解相当复杂
- GMM参数估计
- 注意问题:
- 1.点集的数据结构
- 2.样本的数量
- 3.所采用的距离度量和相似性度量
- 4.聚类准则
- 5.聚类数
- 6.样本各分量之间的尺度比例
- 注意问题:
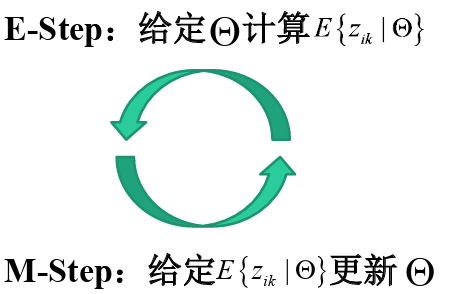
- E-M算法
- 步骤:

- 1.初始化分布参数2.重复直到收敛


- 非监督极大似然估计
- 困难:
- 基于数据的方法
9. 非监督学习
http://binbo-zappy.github.io/2024/12/07/PR-ML/9-非监督学习/