2. 探索与利用

1. 探索与利用

1.1 序列决策任务中的一个基本问题

基于目前策略获取已知最优收益还是尝试不同的决策：

• Exploitation 执行能够获得已知最优收益的决策
• Exploration 尝试更多可能的决策，不一定会是最优收益

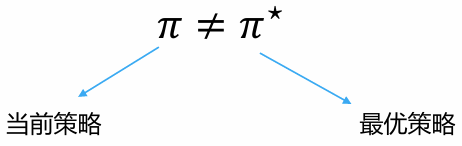
\(\mathcal{E}_t = \left\{ \pi_t^i \mid i = 1, \ldots, n \right\} \xrightarrow{\text{探索}} \mathcal{E}_{t+1} = \left\{ \pi_t^i \mid i = 1, \ldots, n \right\} \cup \left\{ \pi_e^j \mid j = 1, \ldots, m \right\}\)

\(\exists V^* \left( \cdot \mid \pi_t^i \sim \mathcal{E}_t \right) \leq V^* \left( \cdot \mid \pi_{t+1}^i \sim \mathcal{E}_{t+1} \right) \quad \pi_{t+1}^i \sim \left\{ \pi_e^i \mid i = 1, \ldots, m \right\}\)

探索：可能发现更好的策略

1.2 策略探索的一些原则

朴素方法（Naïve Exploration）

• 添加策略噪声𝜖-greedy

积极初始化（Optimistic Initialization）

基于不确定性的度量（Uncertainty Measurement）

• 尝试具有不确定收益的策略，可能带来更高的收益

概率匹配（Probability Matching）

• 基于概率选择最佳策略

状态搜索（State Searching）

• 探索后续状态可能带来更高收益的策略

2. 多臂老虎机

2.1 问题的形式化描述

动作集合：\(a^i \in \mathcal{A}, \quad i = 1, \ldots, K\)

收益（反馈）函数分布：\(\mathcal{R}(r \mid a^i) = \mathbb{P}(r \mid a^i)\)

最大化累积时间的收益：\(\max \sum_{t=1}^{T} r_{t}, \quad r_{t} \sim \mathcal{R}\left(\cdot \mid a_{t}\right)\)

2.2 收益估计

期望收益和采样次数的关系: \(Q_n(a^i) = \frac{r_1 + r_2 + \cdots + r_{n-1}}{n - 1}\)

缺点：每次更新的空间复杂度是O(n)

增量实现: \[ Q_{n+1}(a^i) := \frac{1}{n} \sum_{i=1}^{n} r_i = \frac{1}{n} \left( r_n + \frac{n-1}{n-1} \sum_{i=1}^{n-1} r_i \right) = \frac{1}{n} r_n + \frac{n-1}{n} Q_n = Q_n(a^i) + \frac{1}{n} (r_n - Q_n) \]

空间复杂度为O(1)

2.3 算法：多臂老虎机

1. 初始化：\(Q(a^i) := c^i, \quad N(a^i) = 0, \quad i = 1, ..., n\)
2. 主循环\(t = 1:T\)
   1. 利用策略𝜋选取某个动作a
   2. 获取收益:\(r_t = \text{Bandit}(a)\)
   3. 更新计数器:\(N(a) := N(a) + 1\)
   4. 更新估值:\(Q(a) := Q(a) + \frac{1}{N(a)} [r_t - Q(a)]\)

2.4 应当选取什么样的策略

Regret函数(懊悔值)

• 决策的期望收益：\(Q(a^i) = \mathbb{E}_{r \sim \mathbb{P}(r \mid a^i)}[r]\)

• 最优收益：\(Q^{\star} = \max_{a^i \in \mathcal{A}} Q(a^i)\)

• 决策与最优决策的收益差：\(R(a') = Q^{\star} - Q(a')\)

• Total Regret 函数：\(\sigma_{R} = \mathbb{E}_{a \sim \pi} \left[ \sum_{t=1}^{T} R(a_t^i) \right]\) 越接近于0越好

最小化Total Regret等价于最大化Q值：\(\min \sigma_{R} = \max \mathbb{E}_{a \sim \pi} \left[ \sum_{t=1}^{T} Q(a_{t}^{i}) \right]\)

• 如果一直探索新决策：\(\sigma_{R} \propto T \cdot R\) ,total regret将线性递增，无法收敛
• 如果一直不探索新决策：\(\sigma_{R} \propto T \cdot R\)，total regret 仍将线性递增

是否存在一个方法具有次线性（sublinear）收敛保证的regret？

• 下界
  • 使用\(\Delta_a = Q^* - Q(a)\) 和反馈函数分布相似性：\(D_{KL}\left(\mathcal{R}(r \mid a) \parallel \mathcal{R}^*(r \mid a)\right)\)
  • \(\lim_{T \to \infty} \sigma_R \geq \log T \sum_{a \mid \Delta_a > 0} \frac{\Delta_a}{D_{KL}\left(\mathcal{R}(r \mid a) \parallel \mathcal{R}^*(r \mid a)\right)}\)

2.5 贪心策略和 \(\epsilon\)-greedy 策略

贪心策略

\(Q(a^i) = \frac{1}{N(a^i)} \sum_{t=1}^{T} r_t \cdot 1(a_t = a^i)\)

\(a^* = \arg\max_{a^i} Q(a^i)\)

\(\sigma_R \propto T \cdot [Q(a^i) - Q^*]\)

• 线性增长的 Total regret

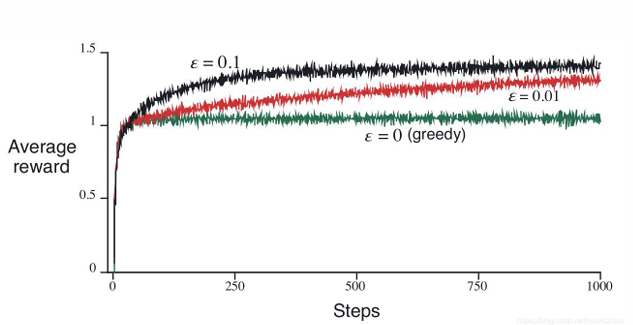
\(\epsilon\)-greedy 策略

\(a_t = \begin{cases} \arg\max_a \hat{Q}(a) & \text{采样概率：} 1 - \epsilon \\ U(0, |\mathcal{A}|) & \text{采样概率：} \epsilon \end{cases}\)

常量 \(\epsilon\) 保证 total regret 满足

\(\sigma_R \geq \frac{\epsilon}{|\mathcal{A}|} \sum_{a \in \mathcal{A}} \Delta_a\)

Total regret 仍然是线性递增的，只是增长率比贪心策略小

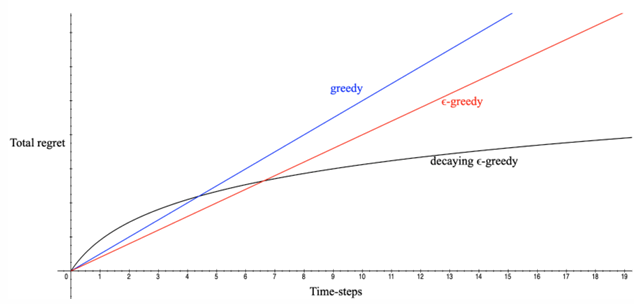
2.6 衰减贪心策略

• \(\epsilon\)-greedy 的变种，\(\epsilon\) 随着时间衰减
• 理论上对数渐进收敛！
• 一种可能的衰减方式：

\[ c \geq 0, \quad d = \min_{a \mid \Delta_a > 0} \Delta_a, \quad \epsilon_t = \min\left\{1, \frac{c|\mathcal{A}|}{d^2 t}\right\} \]

缺点

• 很难找到合适的衰减规划

\(c \geq 0, \quad c_t = \min_{a \mid \Delta_a > 0} \Delta_a, \quad \epsilon_{r_t} = \min\left(1, \frac{c}{c_t^2 \cdot r_t}\right)\)

2.7 不同𝝐-greedy 策略对比：

Total Regret

平均收益

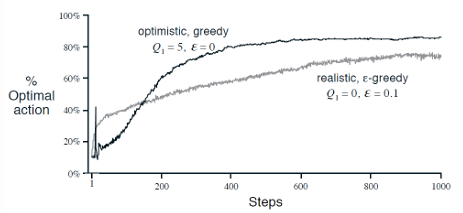
2.8 乐观初始化

• 给\(Q(a^i)\)一个较高的初始化值
• 增量式蒙特卡洛估计更新 \(Q(a^i)\)

\(Q(a^i) := Q(a^i) + \frac{1}{N(a^i)} (r_t - Q(a^i))\)

• 有偏估计，但是随着采样增加，这个偏差带来的影响会越来越小
• 但是仍然可能陷入局部最优

2.9 显式地考虑动作的价值分布

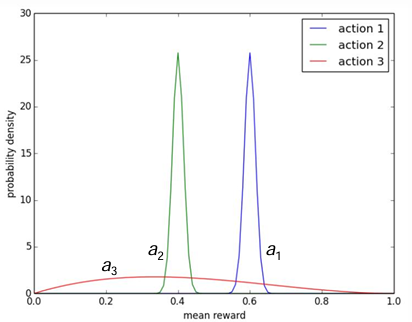
• 考虑以上三个动作的价值分布，平衡探索和利用，选择哪个动作？
• 1. 显式地鼓励不确定性； 2. 直接根据分布采样来选择

2.10 基于不确定性测度

• 不确定性越大的 \(Q(a^i)\)，越具有探索的价值，有可能会是最好的策略
• 一个经验性指导：
  • \(N_{a}\) 大，\(U_{a}\) 小
  • \(N_{a}\) 小，\(U_{a}\) 大
• 策略 \(\pi\)：\(a = \arg\max_{a \in \mathcal{A}} \hat{Q}(a) + \hat{U}(a)\)
• 也称为 UCB：上置信界法（Upper Confidence Bounds）

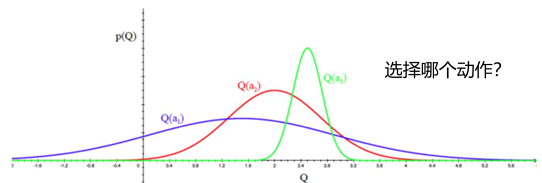
2.11 UCB：上置信界

Hoeffding 不等式：\(\mathbb{P}[\mathbb{E}[x] > \bar{x}_t + u] \leq e^{-2tu^2} \text{ for } x \in [0,1]\)

• 为每个动作收益估值估计一个上置信界：\(\hat{U}(a)\)

• 显然有：\(Q_t(a) \leq \hat{Q}_t(a) + \hat{U}_t(a)\) 以高概率 \(p\) 成立（Hoeffding不等式）

• 依据以下原则挑选进行决策： \[a = \arg\max_{a \in \mathcal{A}} \hat{Q}_t(a) + \hat{U}_t(a) \quad e^{-2N_t(a)U_t(a)^2} = p \Rightarrow \hat{U}_t(a) = \sqrt{-\frac{\log p}{2N_t(a)}}\]

• 收敛性：\(\lim_{t \to \infty} \sigma_R \leq 8 \log t \sum_{a \mid \Delta_a > 0} \Delta_a\)

2.12 Thompson Sampling方法

[Chapelle, Olivier, and Lihong Li. "An empirical evaluation of thompson sampling." Advances in neural information processing systems. 2011.]

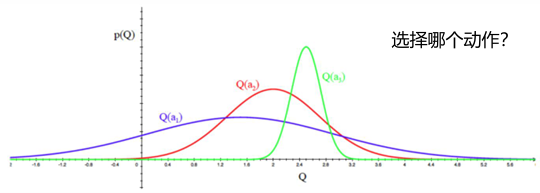
• 想法：根据每个动作成为最优的概率来选择动作

\(p(a) = \int \mathbb{I} \left[ \mathbb{E}_{p(Q(a))} \left[ Q(a; \theta) \right] = \max_{a' \in \mathcal{A}} \mathbb{E}_{p(Q(a'))} \left( Q(a'; \theta) \right) \right] d\theta\)

• 实现：根据当前每个动作 \(a\) 的价值概率分布 \(p(Q(a))\) 来采样到其价值 \(\hat{Q}(a)\)，选择价值最大的动作

2.13 Thompson Sampling和UCB的实验对比

实验：K-arm多臂老虎机，用Beta分布建模每个arm的成功率，初始化成功率分布为Beta(1,1). \[\text{Beta}(x; \alpha, \beta) \propto x^{\alpha-1} (1 - x)^{\beta-1}\]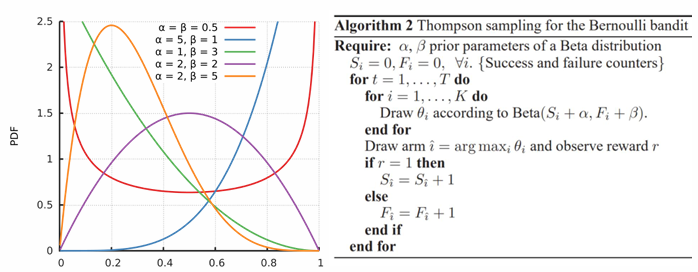

K-arms - The best arm has reward probability of 0.5 - K-1 other arms have the reward probability of 0.5-ε

2.14 探索与利用总结

• 探索与利用是强化学习的 trial-and-error 中的必备技术
• 多臂老虎机可以被看成是无状态 (state-less) 强化学习
• 多臂老虎机是研究探索与利用技术理论的最佳环境
  • 理论的渐近最优 regret 为 \(O(\log T)\)
• \(\epsilon\)-greedy、UCB 和 Thompson Sampling 方法在多臂老虎机任务中十分常用，在强化学习的探索中也十分常用，最常见的是 \(\epsilon\)-greedy