LC509. 斐波那契数列

LC509. 斐波那契数

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

1. 带备忘录的递归解法

即然耗时的原因是重复计算，那么我们可以造一个「备忘录」；

每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

int fib(int N) {
    // 备忘录全初始化为 0
    int memo[N + 1];
    memset(memo, 0, sizeof(memo));
    // 进行带备忘录的递归
    return dp(memo, N);
}

// 带着备忘录进行递归
int dp(int memo[], int n) {
    // base case
    if (n == 0 || n == 1) return n;
    // 已经计算过，不用再计算了
    if (memo[n] != 0) return memo[n];
    memo[n] = dp(memo, n - 1) + dp(memo, n - 2);
    return memo[n];
}

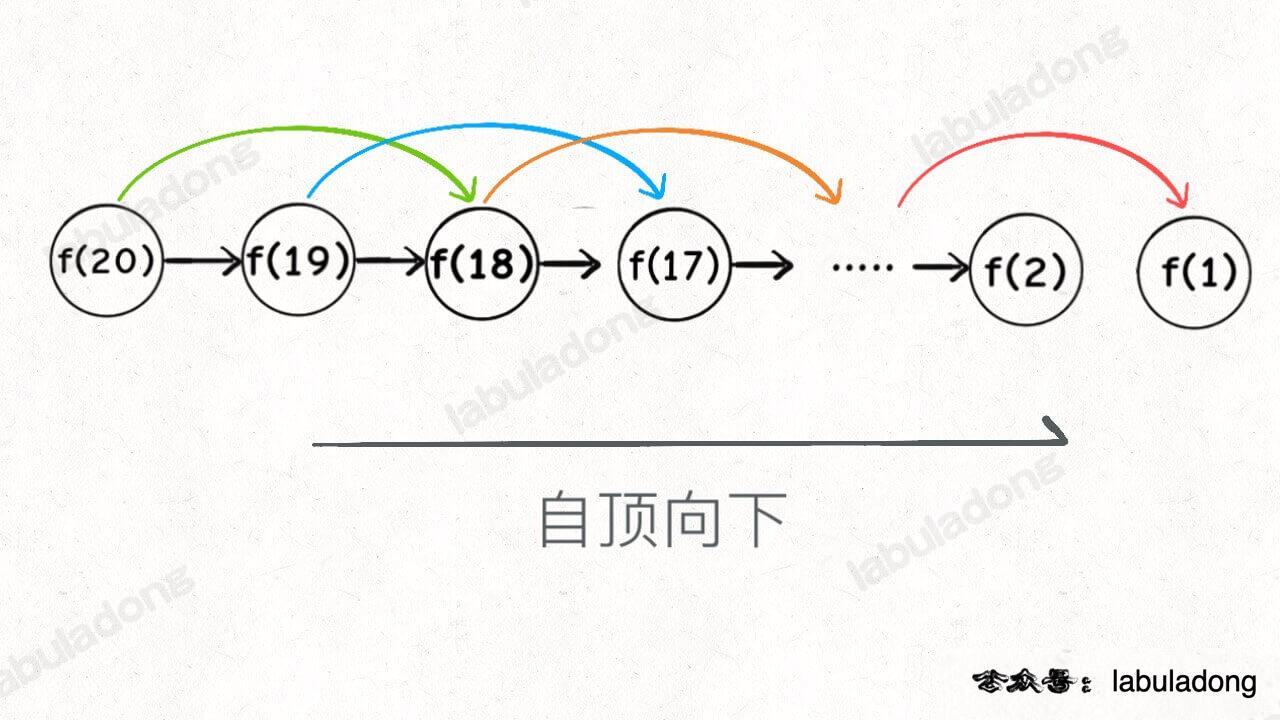
实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。

时空复杂度

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。

子问题个数，即图中节点的总数，由于本算法不存在冗余计算，子问题就是 f(1), f(2), f(3) ... f(20)，数量和输入规模 n = 20 成正比，所以子问题个数为 O(n)。

解决一个子问题的时间，同上，没有什么循环，时间为 O(1)。

所以，本算法的时间复杂度是 O(n)，比起暴力算法，是降维打击。

这段代码实现了一个带备忘录的递归算法来计算斐波那契数列的第 N 项。我们分别分析其时间复杂度和空间复杂度。

1.1 时间复杂度 (Time Complexity)

代码的核心部分是 dp 函数的递归调用。通过使用备忘录（memo 数组），我们可以避免重复计算，每个子问题的解只计算一次。

• 子问题数量：对于计算 fib(N)，我们需要计算 fib(0) 到 fib(N) 共计 N+1 个子问题。
• 每个子问题的计算时间：每个子问题 fib(k) 的计算时间可以认为是 O(1)，因为只需要进行常数时间的加法操作。

因此，总的时间复杂度为子问题数量乘以每个子问题的计算时间： 时间复杂度：O(N)

1.2 空间复杂度 (Space Complexity)

空间复杂度主要考虑两个方面：递归调用栈和备忘录数组。

• 备忘录数组：我们使用了一个大小为 N+1 的数组 memo 来存储中间结果，因此空间复杂度为 O(N)。
• 递归调用栈：在最坏情况下，递归调用的深度为 N（例如，从 fib(N) 递归到 fib(0)），因此递归调用栈的空间复杂度也是 O(N)。

因此，总的空间复杂度为递归调用栈和备忘录数组的空间复杂度之和： 空间复杂度：O(N)

总结

• 时间复杂度：O(N)
• 空间复杂度：O(N)

这种带备忘录的递归算法被称为记忆化搜索（Memoization），它有效地将普通的指数时间复杂度优化为线性时间复杂度。

2. 最终优化解法

进一步优化，把空间复杂度降为 O(1)。这也就是我们最常见的计算斐波那契数的算法：

int fib(int n) {
    if (n == 0 || n == 1) {
        // base case
        return n;
    }
    // 分别代表 dp[i - 1] 和 dp[i - 2]
    int dp_i_1 = 1, dp_i_2 = 0;
    for (int i = 2; i <= n; i++) {
        // dp[i] = dp[i - 1] + dp[i - 2];
        int dp_i = dp_i_1 + dp_i_2;
        // 滚动更新
        dp_i_2 = dp_i_1;
        dp_i_1 = dp_i;
    }
    return dp_i_1;
}

好的，我们来分析一下这个计算斐波那契数列的代码的 时间复杂度 和 空间复杂度。

1. 时间复杂度分析

• 循环次数：
  代码中的 for 循环从 i = 2 开始，直到 i = n，总共运行了 n - 1 次。

• 每次循环的操作：
  每次循环中只进行了常数时间的操作（加法、赋值等），因此每次循环的时间复杂度是 (O(1))。

• 总时间复杂度：
  循环次数乘以每次循环的时间复杂度，即：
  [ T(n) = (n - 1) O(1) = O(n) ]

  因此，时间复杂度为 (O(n))。

---

2. 空间复杂度分析

• 变量使用：
  代码中只使用了固定的几个变量（dp_i_1、dp_i_2、dp_i、i），这些变量的空间占用是常数级别的。

• 额外空间：
  没有使用额外的数据结构（如数组、栈等），空间占用与输入规模 (n) 无关。

• 总空间复杂度：
  空间复杂度是 (O(1))，即常数空间复杂度。

---

总结

• 时间复杂度：(O(n))
  
• 空间复杂度：(O(1))

这个实现是一个典型的 动态规划优化版本，通过滚动数组的思想将空间复杂度从 (O(n)) 优化到了 (O(1))，同时保持了 (O(n)) 的时间复杂度。