第三章 大语言模型基础
第三章 大语言模型基础
1. 语言模型与 Transformer 架构
1.1 从 N-gram 到 RNN
语言模型 (Language Model, LM) 是自然语言处理的核心,其根本任务是计算一个词序列(即一个句子)出现的概率。一个好的语言模型能够告诉我们什么样的句子是通顺的、自然的。
(1) 统计语言模型与N-gram的思想
在深度学习兴起之前,统计方法是语言模型的主流。其核心思想是,一个句子出现的概率,等于该句子中每个词出现的条件概率的连乘。对于一个由词 \(w_1, w_2, \cdots, w_m\) 构成的句子 S,其概率 P(S) 可以表示为:
\[P(S) = P(w_1, w_2, \dots, w_m) = P(w_1) \cdot P(w_2 \mid w_1) \cdot P(w_3 \mid w_1, w_2) \cdot \cdots \cdot P(w_m \mid w_1, \dots, w_{m-1})\]
这个公式被称为概率的链式法则。然而,直接计算这个公式几乎是不可能的,因为像\(P(w_m \mid w_1, \dots, w_{m-1})\)这样的条件概率太难从语料库中估计了,词序列 \(w_1, w_2, \cdots, w_{m-1}\)可能从未在训练数据中出现过。
为了解决这个问题,引入了马尔可夫假设 (Markov Assumption) 核心思想是:我们不必回溯一个词的全部历史,可以近似地认为,一个词的出现概率只与它前面有限的 \(n−1\)个词有关,基于这个假设建立的语言模型,我们称之为 N-gram模型。这些概率可以通过在大型语料库中进行最大似然估计(Maximum Likelihood Estimation,MLE) 来计算。
N-gram 模型定义,基于 “词的出现仅与前 N-1 个词相关” 的假设,N 代表上下文窗口大小,常见的有:
- Bigram(N=2):词的出现仅与前 1 个词相关,即 \(P(w_i \mid w_1, w_2, \dots, w_{i-1}) \approx P(w_i \mid w_{i-1})\)
- Trigram(N=3):词的出现仅与前 2 个词相关,即 \(P(w_i \mid w_1, w_2, \dots, w_{i-1}) \approx P(w_i \mid w_{i-2}, w_{i-1})\)
概率计算方法(最大似然估计):
通过语料库中的词频统计来估算概率,以 Bigram 为例:
\[P(w_i \mid w_{i-1}) = \frac{\text{Count}(w_{i-1}, w_i)}{\text{Count}(w_{i-1})}\]
其中:
- \(\text{Count}(w_{i-1}, w_i)\):词对 \((w_{i-1}, w_i)\)在语料中连续出现的次数
- \(\text{Count}(w_{i-1})\):词 \(w_{i-1}\)在语料中出现的总次数
示例(Bigram 估算句子概率)
用迷你语料 \(\{\text{datawhale agent learns}, \text{datawhale agent works}\}\),估算句子\(\text{datawhale agent learns}\) 的概率:
- 第一步:\(P(\text{datawhale}) = \frac{\text{Count}(\text{datawhale})}{\text{totalCount}} = \frac{2}{6} \approx 0.333\)
- 第二步:$P( ) = = = 1 $
- 第三步:\(P(\text{learns} \mid \text{agent}) = \frac{\text{Count}(\text{agent learns})}{\text{Count}(\text{agent})} = \frac{1}{2} = 0.5\)
- 最终:\(P(\text{datawhale agent learns}) \approx 0.333 \times 1 \times 0.5 = 0.1665\)
N-gram 模型虽然简单有效,但有两个致命缺陷:
- 数据稀疏性 (Sparsity) :如果一个词序列从未在语料库中出现,其概率估计就为 0,这显然是不合理的。虽然可以通过平滑 (Smoothing) 技术缓解,但无法根除。
- 泛化能力差:模型无法理解词与词之间的语义相似性。
(2) 神经网络语言模型与词嵌入
N-gram 模型的根本缺陷在于它将词视为孤立、离散的符号。为了克服这个问题,研究者们转向了神经网络,并提出了一种思想:用连续的向量来表示词。2003年,Bengio 等人提出的前馈神经网络语言模型 (Feedforward Neural Network Language Model) 是这一领域的里程碑。
其核心思想可以分为两步:
- 构建一个语义空间:创建一个高维的连续向量空间,然后将词汇表中的每个词都映射为该空间中的一个点。这个点(即向量)就被称为词嵌入
(Word Embedding)
或词向量。在这个空间里,语义上相近的词,它们对应的向量在空间中的位置也相近。例如,
agent和robot的向量会靠得很近,而agent和apple的向量会离得很远。 - 学习从上下文到下一个词的映射:利用神经网络的强大拟合能力,来学习一个函数。这个函数的输入是前 \(n−1\) 个词的词向量,输出是词汇表中每个词在当前上下文后出现的概率分布。
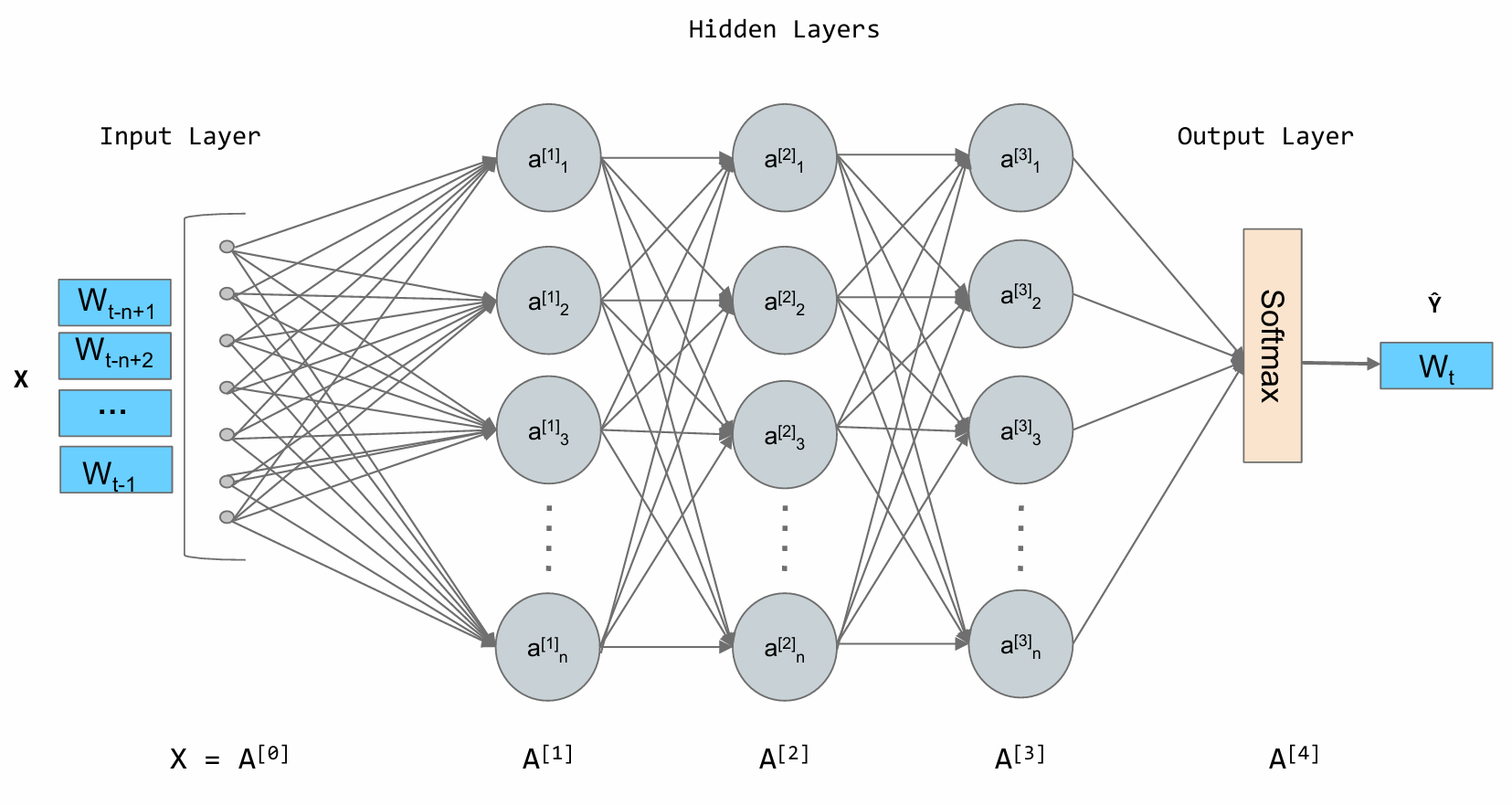
词嵌入是在模型训练过程中自动学习得到的。模型为了完成“预测下一个词”这个任务,会不断调整每个词的向量位置,最终使这些向量能够蕴含丰富的语义信息。一旦我们将词转换成了向量,我们就可以用数学工具来度量它们之间的关系。最常用的方法是余弦相似度 (Cosine Similarity) ,它通过计算两个向量夹角的余弦值来衡量它们的相似性。
\[\text{similarity}(\vec{a}, \vec{b}) = \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}\]
这个公式的含义是:
- 如果两个向量方向完全相同,夹角为0°,余弦值为1,表示完全相关。
- 如果两个向量方向正交,夹角为90°,余弦值为0,表示毫无关系。
- 如果两个向量方向完全相反,夹角为180°,余弦值为-1,表示完全负相关。
通过这种方式,词向量不仅能捕捉到“同义词”这类简单的关系,还能捕捉到更复杂的类比关系。
(3)循环神经网络 (RNN) 与长短时记忆网络 (LSTM)
循环神经网络 (Recurrent Neural Network, RNN) 为网络增加“记忆”能力。标准的 RNN 在实践中存在长期依赖问题 (Long-term Dependency Problem) 。当序列很长时,梯度在从后向前传播的过程中会经过多次连乘,这会导致梯度值快速趋向于零(梯度消失)或变得极大(梯度爆炸)。梯度消失使得模型无法有效学习到序列早期信息对后期输出的影响,即难以捕捉长距离的依赖关系。
LSTM 是一种特殊的 RNN,其核心创新在于引入了细胞状态 (Cell State) 和一套精密的门控机制 (Gating Mechanism) 。细胞状态可以看作是一条独立于隐藏状态的信息通路,允许信息在时间步之间更顺畅地传递。门控机制则是由几个小型神经网络构成,它们可以学习如何有选择地让信息通过,从而控制细胞状态中信息的增加与移除。这些门包括:
- 遗忘门 (Forget Gate):决定从上一时刻的细胞状态中丢弃哪些信息。
- 输入门 (Input Gate):决定将当前输入中的哪些新信息存入细胞状态。
- 输出门 (Output Gate):决定根据当前的细胞状态,输出哪些信息到隐藏状态。
1.2 Transformer 架构解析
(1)Encoder-Decoder 整体结构
最初的 Transformer 模型是为端到端任务机器翻译而设计的。如图所示,在宏观上遵循了一个经典的编码器-解码器 (Encoder-Decoder) 架构。
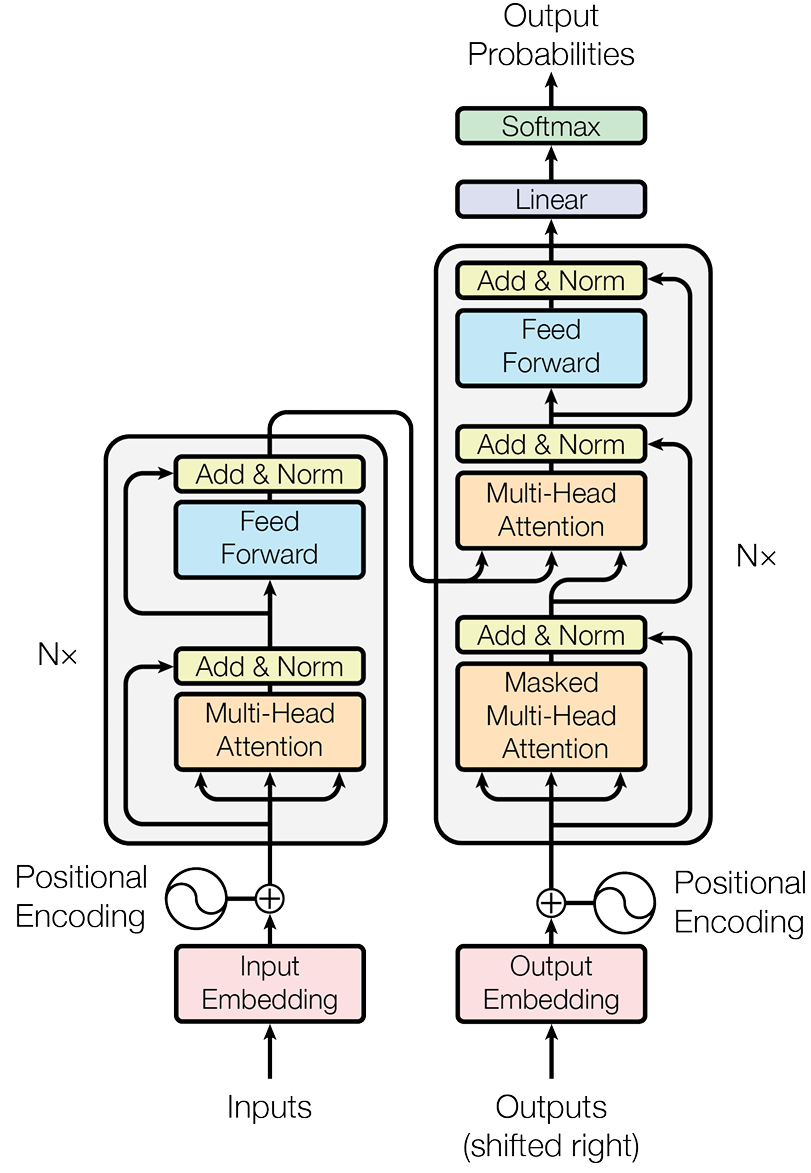
我们可以将这个结构理解为一个分工明确的团队:
- 编码器 (Encoder) :任务是“理解”输入的整个句子。它会读取所有输入词元(这个概念会在3.2.2节介绍),最终为每个词元生成一个富含上下文信息的向量表示。
- 解码器 (Decoder) :任务是“生成”目标句子。它会参考自己已经生成的前文,并“咨询”编码器的理解结果,来生成下一个词。